©Richard Lowry, 1999-
All rights reserved.
Subchapter 3a.
Partial Correlation
Suppose you were to measure each of N subjects on each of three variables, X, Y, and Z, and find the following correlations:
| X versus Y: | rXY = +.50 | r2XY = .25
|
| X versus Z:
| rXZ = +.50
|
| r2XZ = .25
|
| Y versus Z:
| rYZ = +.50
|
| r2YZ = .25
|
| |
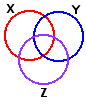
Note as well that there is one region where all three of the variability circles overlap. The meaning of this three-
Partial correlation is a procedure that allows us to measure the region of three-
| rXY·Z = | rXY—(rXZ)(rYZ) sqrt[1—r2XZ] x sqrt[1—r2YZ] |
which for the present example would work out as
| rXY·Z = | .50—(.50)(.50) sqrt[1—.25] x sqrt[1—.25]
|
| rXY·Z = | +.33 |
|
|
| Hence r2XY·Z = .11 | |
The same general structure would apply for calculating the partial correlation of X and Z, with the effects of Y removed:
| rXZ·Y = | rXZ—(rXY)(rYZ) sqrt[1—r2XY] x sqrt[1—r2YZ] |
and for for calculating the partial correlation of Y and Z, with the effects of X removed:
| rYZ·X = | rYZ—(rXY)(rXZ) sqrt[1—r2XY] x sqrt[1—r2XZ] |
Here is the apparatus of partial correlation applied to a real-
| C versus A: | rCA = +.49 | r2CA = .24
|
| C versus V:
| rCV = +.73
|
| r2CV = .53
|
| A versus V:
| rAV = +.59
|
| r2AV = .35
|
| |
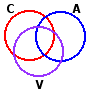
Here the overlaps are less evenly proportioned, although the logic is quite the same. Of the 24% variance overlap that occurs in the relationship between comprehension and arithmétic ability, a substantial portion reflects the fact that both of these variables are correlated with vocabulary. If we were to remove the effects of vocabulary from the relationship between C and A, the resulting partial correlation would be
| rCA·V = | rCA—(rCV)(rAV) sqrt[1—r2CV] x sqrt[1—r2AV] |
| rCA·V = | .49—(.73)(.59) sqrt[1—.53] x sqrt[1—.35]
|
| rCA·V = | +.11 |
|
|
| Hence r2CA·V = .01 | |
In brief: with the effects of vocabulary removed, the correlation between comprehension and arithmétic ability collapses down to hardly anything at all. The practical inference is that if we were to administer the WAIS to a sample of subjects who were homogeneous with respect to breadth of vocabulary, the correlation between their scores on the comprehension and arithmétic sub-
In most cases a partial correlation of the general form rXY·Z will turn out smaller than the original correlation rXY. In those cases where it turns out larger, the third variable, Z, is typically spoken of as a supressor variable on the assumption that it is suppressing the larger correlation that would appear between X and Y if Z were held constant.
Suppose, for example, that a rather cranky professor has just administered an exam in his statistics course, and that for each student in the course we have measures on each of the following three variables:
| X = | the amount of effort spent on studying for the exam beforehand|
| Y = | the student's score on the exam |
| Z = | a measure of the degree to which the professor inspires fear and trembling in the student | |
And here are the correlations among the three variables:
| X versus Y: | rXY = +.20 | r2XY = .04
|
| X versus Z:
| rXZ = +.80
|
| r2XZ = .64
|
| Y versus Z:
| rYZ = —.40
|
| r2YZ = .16
|
| |
| rXY·Z = | .20—(.80)(—.40) sqrt[1—.64] x sqrt[1—.16] |
| |||
| rXY·Z = | +.95|
| |
The VassarStats computational site includes a page that will calculate the partial correlation coefficients for any particular set of three intercorrelated variables.
End of Subchapter 3a.
Return to Top of Subchapter 3a
Go to Subchapter 3b [Rank-Order Correlation]
Go to Chapter 4 [A First Glance at the Question of Statistical Significance]
| Home | Click this link only if the present page does not appear in a frameset headed by the logo Concepts and Applications of Inferential Statistics |