The version of correlation examined in the main body of Chapter 3 applies to those cases where the values of X and of Y are both measured on an equal- interval scale. It is also possible to apply the apparatus of linear correlation to cases where X and Y are measured on a merely ordinal scale. When applied to ordinal data, the measure of correlation is spoken of as the Spearman rank- order correlation coefficient, typically symbolized as r_s.

Suppose, for example, that two experts, X and Y, were asked to rank N=8 items with respect to some dimension germane to their field of expertise (rank#1=highest, rank#8=lowest). To make it specific, you can imagine two physicians ranking 8 patients with respect to the severity of their disease; two psychotherapists ranking 8 patients with respect to the likelihood of improvement; two wine experts ranking 8 wines from best to worst; two statisticians ranking 8 statistical concepts with respect to their fundamental importance; or whatever else it might be that strikes your fancy.

As a token of my liberal-mindedness—for I am one of those benighted souls who find all wines to taste suspiciously like vinegar—I will use the image of the wine experts. The following table shows the rankings from 1 to 8, best to worst, of two experts, X and Y.

wine	X	Y
a  b  c  d  e  f  g  h	1 2 3 4 5 6 7 8	2 1 5 3 4 7 8 6

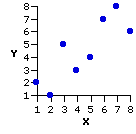
As you can see from the accompanying graph, there is a substantial degree of agreement between the rankings of the two experts. Plug the bivariate values of X and Y into the formulaic structure given in the main body of Chapter 3,

	r =	SCXY sqrt[SSX x SSY]		and you will find   r = +.83   r2 = .69.

As it happens, these are exactly the same values you will get when you calculate the Spearman coefficient, r_s. The simple reason for this is that r and r_s are algebraically equivalent in the case where the values of X and Y consist of two sets of N rankings. The only advantage of r_s is that the calculations are easier if you are doing them by hand. [Note, however, that r_s is precisely equal to r only when the rankings within X and Y are the consecutive integer values: 1, 2, 3, and so on, with no ties. With tied ranks there will tend to be discrepancies between r_s and r. If the proportion of tied ranks is fairly large, you would be better advised to plug your rankings for X and Y into the standard formula for r.]

The Simple Formula for r_s, for Rankings without Ties

wine	X	Y	D	D2
a  b  c  d  e  f  g  h	1 2 3 4 5 6 7 8	2 1 5 3 4 7 8 6	—1 1 —2 1 1 —1 —1 2	1 1 4 1 1 1 1 4
N = 8-∑D2 = 14

Here is the same table you saw above, except now we also take the difference between each pair of ranks (D=X—Y), and then the square of each difference. All that is required for the calculation of the Spearman coefficient are the values of N and-∑D², according to the formula

rs

=

1 —

6∑D2 N(N2—1)

If this formula seems a bit odd to you, you are in good company. Generations of statistics students have been presented with it, and generations have puzzled over such mind- bending questions as: why do you start out with "1" and subtract something from it?; where does that N(N²—1) in the denominator come from?; and, above all, how does that peculiar "6" get into the numerator?

Here are the answers to these age-old questions in a nutshell.

• For any set of N paired bivariate ranks, the minimum possible value of-∑D² occurs in the case of perfect positive correlation. In this case, rank 1 for X is paired with rank 1 for Y, rank 2 for X with rank 2 for Y, and so on. Each value of D will accordingly be equal to zero, and so too will be the sum of the squared values of D.

• Conversely, the maximum possible value of-∑D² occurs in the case of perfect negative correlation. This maximum possible value is in every instance equal to
  

  	maximum-∑D2 =	N(N2—1) 3

  
  Thus, for N=8 with perfect negative correlation:_T
  

  item	X	Y	D	D2	-∑D2 = 168   8(82—1)/3 = 168
  a  b  c  d  e  f  g  h	1 2 3 4 5 6 7 8	8 7 6 5 4 3 2 1	—7 —5 —3 —1 1 3 5 7	49 25 9 1 1 9 25 49

  
  
• The ratio of the observed-∑D² to its maximum possible value will therefore be equal to zero in the case of perfect positive correlation, to +1.0 in the case of perfect negative correlation, and to +.50 in the case of zero correlation.

  -∑D2 N(N2—1)/3

  =

  3∑D2 N(N2—1)

  
  Double this ratio, subtract it from 1, and voila! you have a quantity that will be equal to +1.0 in the case of perfect positive correlation, to —1.0 in the case of perfect negative correlation, and to zero in the case of zero correlation.

  rs

  =

  1 —

  6∑D2 N(N2—1)

  
  

And here, finally, is the calculation of r_s for the example with which we began:

wine	X	Y	D	D2
a  b  c  d  e  f  g  h	1 2 3 4 5 6 7 8	2 1 5 3 4 7 8 6	—1 1 —2 1 1 —1 —1 2	1 1 4 1 1 1 1 4
N = 8-∑D2 = 14

	rs	=	1 —	6∑D2 N(N2—1)
		=	1 —	6 x 14 8(82—1)
		= +.83
	r2s	= .69

The meanings of r_s and r²_s in a rank- order correlation are essentially the same as those of r and r² in a correlation based on equal- interval data. For the present example, r²_s=.69 means that the covariance between the X and Y rankings is 69% as strong as it possibly could be, and the positive sign of r_s=+.83 signals that this covariation occurs along the upward slant, with higher values of X tending to be associated with higher values of Y, and vice versa. However, I would not recommend taking the parallels much farther than this. In particular, I think it would not make much sense to subject bivariate rankings to the predictive apparatus of linear regression.

---