Subject	Sample A shoes on	Sample B shoes off
1  2  3  4  5  6  7  8  9  10  11  12  13  14  15	64.8 70.5 69.3 55.5 61.4 69.7 68.8 64.6 63.8 61.9 69.4 63.0 75.5 69.4 59.1	63.5 68.8 67.6 54.1 59.9 68.6 66.7 63.0 61.8 59.4 68.4 61.1 73.9 68.2 58.1
mean	65.8	64.2	MA — MB = 1.6
SS	378.4	384.1
variance	25.2	25.6
standard deviation	±5.0	±5.1

A certain researcher developed the inspired hypothesis that people are taller when they are wearing shoes than when they are not wearing shoes. To test this hypothesis, he took a random sample of 15 adults, measuring the height of each individual subject first with shoes on, and then again with shoes off. The result was two samples of height measures, A and B, of sizes N_a=15 and N_b=15. The adjacent table shows the shoes-on and shoes-off measures of height, in inches, for each subject.

Aha! says the investigator. The null hypothesis here is that the distance from the top of a person's head to the horizontal surface on which he or she erectly stands is unrelated to whether the person is wearing shoes. I, on the other hand, have begun with the directional hypothesis that people are in fact taller with shoes on than with shoes off—and the outcome of my experiment is clearly consistent with that hypothesis. On average, my subjects were 1.6 inches taller when they had their shoes on than when they took them off. Moreover, each individual subject, without exception, was taller with shoes on than with shoes off.

Well, you're right, of course. The word to describe our investigator's hypothesis is not "inspired," but "banal." People obviously are taller with their shoes on than with their shoes off, and one hardly needs the labors of science to prove that commonplace. But please bear with me a moment, for the general structure of this example is illustrative of a wide range of real-life research situations where the questions are by no means trivial and the answers are not at all obvious in advance. The point I want to make with it is that, if you were to plug the data from the above table into the independent-samples t-test described in Chapter 11, you would find the 1.6 inch difference between the means of the two sets of measures to be non-significant by a substantial margin (t=+0.84, df=28; for significance at the basic .05 level for a directional test, the observed value of t would have to be at least 1.70). Clearly people are taller when shod than when unshod—but the t-test for independent samples is unable to detect that simple fact. It would have us conclude that the mean difference between the shoes-on and shoes-off conditions could easily have occurred through mere chance coincidence.

The reason for this oddity can be approached through the relationship shown in Figure 12.1 below. The blue circles in the top row show the measures of height for individual subjects with shoes on, and those in the bottom row show the measures with shoes off. Notice in particular that the difference between the means of these two sets of measures is rather tiny in comparison with the variability (the spread of the circles in each row) that exists inside the two sets.

Figure 12.1. Distributions of Samples A and B

 

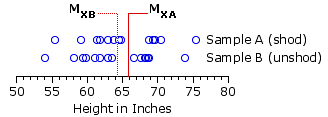
The import of this relationship—small mean difference versus large internal variability—can be seen by looking closely at what is going on inside the independent-samples t-test.

t

=

MXa—MXb est.iM-M

Formula for independent-samples t-test, from Ch. 11.

As laid out in Chapter 11, the denominator in this formula derives ultimately from SS_A and SS_B, the raw measures of variability that exists inside the two samples. Hence, the greater the amount of variability there is within the two samples, the larger will be the denominator; and the smaller, accordingly, will be the value of t. This is no mere game of numbers. The variability that exists inside samples A and B in this situation reflects nothing other than the fact that there are substantial individual differences among people with respect to the variable of height. A person who is relatively tall without shoes will also be relatively tall with shoes. A person who is relatively short without shoes will also be relatively short with shoes. The only difference between the respective variabilities of the two sets of measures will be occasioned by the differing amounts by which their shoes raise them off the floor. If all subjects had worn shoes of identical height, the respective variabilities of the two samples would be identical.

The point here is that these pre-existing individual differences with respect to height are entirely extraneous to the question of whether people on average are taller with shoes than without. The t-test for independent samples treats this extraneous variability as though it were not extraneous, and in consequence it overestimates the standard deviation of the relevant sampling distribution. That, in turn, results in an underestimate of the significance of the observed mean difference. The procedure to be introduced in the present chapter avoids this pitfall by disregarding the extraneous variability and looking only at what is relevant to the question at hand.

This procedure is spoken of as the t-test for correlated samples, for the simple reason that the two sets of measures in such a situation are arranged in pairs and are thus potentially correlated. You will also find this procedure spoken of as the repeated-measures or within-subjects t-test, because it typically involves situations in which each subject is measured twice, once in condition A, and then again in condition B. However, it is not essential that the measures in conditions A and B come from the same subjects. You could equally well start out with matched pairs of subjects (to be illustrated in a moment). The only requirement of the correlated-samples design, vis-à-vis the structure of the data, is that each individual item in sample A is intrinsically linked with a corresponding item in sample B. The height of subject 1 while wearing shoes is linked with the height of subject 1 while not wearing shoes; and so, too, for subjects 2 through 15.

Indeed, insofar as we are concerned only with the difference between the shoes-on and shoes-off conditions, there is really only one sample here. The variable in this single sample can be denoted as D (for "difference") and defined for each linked pair as

D_i = X_Ai — X_Bi

where X_Ai is the height measure for subject i (i = 1, 2, 3, etc.) in the shoes-on condition and X_Bi is the height measure for the same subject in the shoes-off condition.

Subject	Sample A shoes on	Sample B shoes off	Di
1  2  3  4  5  6  7  8  9  10  11  12  13  14  15	64.8 70.5 69.3 55.5 61.4 69.7 68.8 64.6 63.8 61.9 69.4 63.0 75.5 69.4 59.1	63.5 68.8 67.6 54.1 59.9 68.6 66.7 63.0 61.8 59.4 68.4 61.1 73.9 68.2 58.1	+1.3 +1.7 +1.7 +1.4 +1.5 +1.1 +2.1 +1.6 +2.0 +2.5 +1.0 +1.9 +1.6 +1.2 +1.0
Recall thatx  Di=XAi— XBi		MD	1.6
		SSD	2.59
		variance	0.17
		standard deviation	±0.42

The table to the right shows the same data you saw earlier, but now with the calculation of D for each subject. Notice that while the mean of all these D-values, M_D=1.6, is precisely the same as the difference we noted above between M_A and M_B, we now have much smaller measures of variability.

From this point on, the logic of the situation will be familiar. If there were no tendency for people to be taller with shoes than without, then we would expect the mean of the D-values in such a sample to approximate zero. The question, therefore, is whether our observed value of M_D=1.6 is significantly different from zero. Once again, it is a task of determining where the observed fact falls within the appropriate sampling distribution.

The t-test for correlated samples is especially useful in research involving human or animal subjects precisely because it is so very effective in removing the extraneous effects of pre-existing individual differences. This is not to suggest that individual differences are "extraneous" in every context. In some cases they might be the very essence of the phenomena that are of interest. But there are also situations where the facts that are of interest are merely obscured by the variability of individual differences. I will illustrate the point with another example involving two types of music, roughly analogous to the example considered in Chapter 11. Suppose we were interested in determining whether two types of music, A and B, differ with respect to their effects on sensory-motor coordination. One way to approach the question would be to assemble two separate, independent samples of human subjects, measuring the members of one group on a task of sensory-motor coordination performed in the presence of type-A music, and the members of the other group on the same task in the presence of type-B music.

However, if your life, fame, fortune, or tenure depend on ending up with a significant result, this would probably not be a good strategy. For even if the two types of music do, in reality, have different effects, the difference would probably be eclipsed by the pre-existing individual differences among your subjects. Much of this variability would stem from inherent differences in sensory-motor coordination itself, although one can readily imagine other kinds of individual differences as well, such as motivation for this particular task, anxiety in test situations, ability to work under pressure, prior adaptation to one or the other type of music, and so on. In any event, it would be completely extraneous to the simple question of whether the two types of music have different effects on sensory-motor coordination.

With a research design involving two correlated samples on the other hand, we can hold the obscuring effects of such individual differences to a bare minimum. In the design involving independent samples, we test some subjects in the presence of type-A music and other subjects in the presence of type-B music. With the design for correlated samples we test all subjects in both conditions and focus on the difference between the two measures for each subject. To obviate the potential effects of practice and test sequence in this case, we would also want to arrange that half the subjects are tested first in the type-A condition, then later in the type-B condition, and vice versa for the other half.

Suppose we were actually to conduct an experiment of this sort with a sample of 15 subjects, measuring how well each subject performs the task of sensory-motor coordination in each of the two conditions. We begin with the expectation that the two types of music might have different effects on sensory-motor coordination, though we have no particular hunches about the likely direction of the difference. Our research hypothesis is therefore non-directional.

	Music Type
Subject	A	B	Di
1  2  3  4  5  6  7  8  9  10  11  12  13  14  15	10.2  8.4  17.8  25.2  23.8  25.7  16.2  21.5  21.1  16.9  24.6  20.4  25.8  17.1  14.4	13.2  7.4  16.6  27.0  27.5  26.6  18.0  21.2  23.4  21.1  23.8  20.2  29.1  17.7  19.2	.—3.0  +1.0  +1.2  .—1.8  .—3.7  .—0.9  .—1.8  +0.3  .—2.3  .—4.2  +0.8  +0.2  .—3.3  .—0.6  .—4.8
Recall thatx  Di=XAi— XBi		MD	.—1.53
		SSD	55.45
		variance	3.70
		standard deviation	±1.92

The next table (also to the right) shows the measures we end up with, along with the relevant summary statistics. We will stipulate that the measures of task performance in columns A and B derive from an equal-interval scale; the measures of D are therefore also on an equal-interval scale. In the column of D-values, a positive sign indicates that the subject's performance on the task was better in condition A than in condition B, while a negative sign indicates the opposite. As you can see, the negative signs preponderate, suggesting at first glance that sensory-motor coordination is on average better with music of type-B than with music of type-A. This, of course, is also what is suggested by the observed value of M_D=—1.53. All that remains is to determine whether this observed value significantly differs from the zero that would have been expected on the basis of the null hypothesis.

---

¶Logic and Procedure

The groundwork for each of the following points, except the first, is laid down in Chapter 9.

(1)	According to the null hypothesis, the values of Di in the sample derive from a source population whose mean is

isource = 0

(2)	If we knew the variance of the source population, we would then be able to calculate the standard deviation ("standard error") of the sampling distribution of MD as

xMD = sqrt

[

x2source   N

]

From Ch.9, Pt.1

(3)	This, in turn, would allow us to test the null hypothesis for any particular instance of MD by calculating the appropriate z-ratio

z =

MD MD

From Ch.9, Pt.1

(3)	and referring the result to the unit normal distribution. In actual practice, however, the variance of the source population of D-values, hence also the value of iMD, can be arrived at only through estimation. In these cases the test of the null hypothesis is performed not with z but with t:

t

=

MD est.iMD

From Ch.9, Pt.2

(3)	The resulting value belongs to the particular sampling distribution of t that is defined by df=N—1, where N is the number of D-values.

(3)	For this next point, recall that the relevant numerical values for the present example are N=15, MD=—1.53, and SSD=55.45.
	As indicated in Chapter 9, the variance of the source population can be estimated as

{s2}

=

SSD N—1

From Ch.9, Pt.2

(3)	which for the present example comes out as

{s2}

=

55.45 14

= 3.96

(3)	This, in turn, allows us to estimate the standard deviation of the sampling distribution of MD as

	est.iMD = sqrt	[	{s2} N	]	From Ch.9, Pt.2
	= sqrt	[	3.96 15	]	= ±0.51

(4)	The estimated value ofiMD then permits the calculation of t as

	it	=i	MD est.iMD
		=	.—1.53 0.51	= —3.0with df=14

---

¶Inference

Figure 12.2 shows the outline and numerical details (cf. Appendix C) of the sampling distribution of t for df=14. We started out with a non-directional research hypothesis, so the relevant critical values of t are those that pertain to a non-directional, two-tailed test of significance: 2.15 for the .05 level of significance, 2.62 for the .02 level, 2.98 for the .01 level, and so on. For purposes of a two-tailed test, the observed value of t=—3.0 must be conceived of as t=±3.0.

Figure 12.2. Sampling Distribution of t for df=14
  

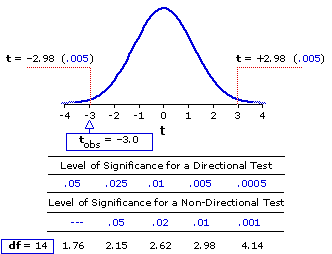
Our observed t meets and slightly exceeds the critical value for the .01 level, hence can be regarded as significant slightly beyond the .01 level. Here again, the practical, bottom-line meaning of such a conclusion is that the likelihood of our experimental result having come about through mere chance coincidence is a bit less that 1%. So we can be quite confident, at the level of about 99%, that it reflects something more than mere random variability. If we had started out with the directional hypothesis that performance would be better under condition B, we would have performed a one-tailed test and found the result to be significant beyond the .005 level.

---

¶Step-by-Step Computational Procedure: t-Test for the Significance of the Difference between the Means of Two Correlated Samples

---

Step 1. For the sample of N values of D_i, where each instance of D_i is equal to X_Ai—X_Bi, calculate the mean of the sample as

MD =

i∑Dii Ni

and the sum of squared deviates as

SSD =i∑D2i —

(i∑Di)2 iNi

---

Step 2. Estimate the variance of the source population as

{s2}

=

SSD N—1

---

Step 3. Estimate the standard deviation of the sampling distribution of M_D as

est.MD

=i

sqrti

[

{s2} iNi

]

---

Step 4. Calculate t as

it

=i

MD est.iMD

---

Step 5. Refer the calculated value of t to the table of critical values of t (Appendix C), with df=N—1. Keep in mind that a one-tailed directional test can be applied only if a specific directional hypothesis has been stipulated in advance; otherwise it must be a non-directional two-tailed test.

---

So as not to leave you lying awake at night wondering about it, I'll conclude by noting that if you were to apply the correlated-samples t-test to the data of the shoes-on versus shoes-off example, you would find the observed value of M_D=+1.6 to be very significant indeed (t=+14.17, df=14). If the null hypothesis were true—if it makes no difference in height whether a person is shod or unshod—the one-tailed probability of ending up with a value of M_D this large or larger by mere chance coincidence would be a miniscule 0.0000000005. (In Figure 12.2, above, you can see that t=+14.17 for df=14 falls way outside the visible portion of the scale.)

---

Note that this chapter includes a subchapter on the Wilcoxon Signed-Rank Test, which is a non-parametric alternative to the correlated-samples t-test.