©Richard Lowry, 1999-
All rights reserved.

Subchapter 12a.
The Wilcoxon Signed-Rank Test

In Subchapter 11a we examined a non-parametric alternative to the t-test for independent samples. We now turn to consider a somewhat analogous alternative to the t-test for correlated samples. As indicated in the main body of Chapter 12, the correlated-samples t-test makes certain assumptions and can be meaningfully applied only insofar as these assumptions are met. Namely,
  1. that the scale of measurement for XA and XB has the properties of an equal-interval scale;T
  2. that the differences between the paired values of XA and XB have been randomly drawn from the source population; andT
  3. that the source population from which these differences have been drawn can be reasonably supposed to have a normal distribution.
Here again, it is not simply a question of good manners or good taste. If there is one or more of these assumptions that we cannot reasonably suppose to be satisfied, then the t-test for correlated samples cannot be legitimately applied.

Of all the correlated-samples situations that run afoul of these assumptions, I expect the most common are those in which the scale of measurement for XA and XB cannot be assumed to have the properties of an equal-interval scale. The most obvious example would be the case in which the measures for XA and XB derive from some sort of rating scale. In any event, when the data within two correlated samples fail to meet one or another of the assumptions of the t-test, an appropriate non-parametric alternative can often be found in the Wilcoxon Signed-Rank Test.

To illustrate, suppose that 16 students in an introductory statistics course are presented with a number of questions (of the sort you encountered in Chapters 5 and 6) concerning basic probabilities. In each instance, the question takes the form "What is the probability of such-and-such?" However, the students are not allowed to perform calculations. Their answers must be immediate, based only on their raw intuitions. They are instructed to frame each answer in terms of a zero to 100 percent rating scale, with 0% corresponding to P=0.0, 27% corresponding to P=.27, and so forth. They are also told that they can give non-integer answers if they wish to make really fine-grained distinctions; for example, 49.0635...%. (As it turns out, none do.)

The instructor of the course is particularly interested in student's responses to two of the questions, which we will designate as question A and question B. He reasons that if students have developed a good, solid understanding of the basic concepts, they will tend to give higher probability ratings for question A than for question B; whereas, if they were sleeping through that portion of the course, their answers will be mere shots in the dark and there will be no overall tendency one way or the other. The instructor's hypothesis is of course directional: he expects his students have mastered the concepts well enough to sense, if only intuitively, that the event described in question A has the higher probability. The following table shows the probability ratings of the 16 subjects for each of the two questions.

Subj.
 XA 
 XB 
XA—XB
1 
2 
3 
4 
5 
6 
7 
8 
9 
10 
11 
12 
13 
14 
15 
16 
 78
24
64
45
64
52
30
50
64
50
78
22
84
40
90
72
 78
24
62
48
68
56
25
44
56
40
68
36
68
20
58
32
 0
0
+2
—3
—4
—4
+5
+6
+8
+10
+10
—14
+16
+20
+32
+40
mean difference = +7.75

Voilà! The observed results are consistent with the hypothesis. The probability ratings do on average end up higher for question A than for question B. Now to determine whether the degree of the observed difference reflects anything more than some lucky guessing.

¶Mechanics

The Wilcoxon test begins by transforming each instance of XA—XB into its absolute value, which is accomplished simply by removing all the positive and negative signs. Thus the entries in column 4 of the table below become those of column 5. In most applications of the Wilcoxon procedure, the cases in which there is zero difference between XA and XB are at this point eliminated from consideration, since they provide no useful information, and the remaining absolute differences are then ranked from lowest to highest, with tied ranks included where appropriate.
The guidelines for assigning tied ranks are
described in Subchapter 11a in connection
with the Mann-Whitney test.
The result of this step is shown in column 6. The entries in column 7 will then give you the clue to why the Wilcoxon procedure is known as the signed-rank test. Here you see the same entries as in column 6, except now we have re-attached to each rank the positive or negative sign that was removed from the XA—XB difference in the transition from column 4 to column 5.

1
2
3
4
5
6
7
Subj.
 XA 
 XB 
original
XA—XB
absolute
XA—XB
rank of
absolute
 XA—XB
signed
rank
1 
2 
3 
4 
5 
6 
7 
8 
9 
10 
11 
12 
13 
14 
15 
16 
 78
24
64
45
64
52
30
50
64
50
78
22
84
40
90
72
 78
24
62
48
68
56
25
44
56
40
68
36
68
20
58
32
 0
0
+2
—3
—4
—4
+5
+6
+8
+10
+10
—14
+16
+20
+32
+40
 0
0
2
3
4
4
5
6
8
10
10
14
16
20
32
40
 ---
---
1
2
3.5
3.5
5
6
7
8.5
8.5
10
11
12
13
14
 ---
---
+1
—2
—3.5
—3.5
+5
+6
+7
+8.5
+8.5
—10
+11
+12
+13
+14
W = 67.0 
TN = 14 

The sum of the signed ranks in column 7 is a quantity symbolized as W, which for the present example is equal to 67. Two of the original 16 subjects were removed from consideration because of the zero difference they produced in columns 4 and 5, so our observed value of W is based on a sample of size N=14.

¶Logic & Procedure

Here again, as with the Mann-Whitney test, the effect of replacing the original measures with ranks is two-fold. The first is that it brings us to focus only on the ordinal relationships among the measures—"greater than," "less than," and "equal to"—with no illusion that these measures have the properties of an equal-interval scale. And the second is that it transforms the data array into a kind of closed system whose properties can then be known by dint of sheer logic.

For openers, we know that the sum of the N unsigned ranks in column 6 will be equal to

sum
=
N(N+1)
2
From Subchapter 11a
=
14(14+1)
2
= 105

Thus the maximum possible positive value of W (in the case where all signs are positive) is W=+105, and the maximum possible negative value (in the case where all signs are negative) is W=—105. For the present example, a preponderance of positive signs among the signed ranks would suggest that subjects tend to rate the probability higher for question A than for question B. A preponderance of negative signs would suggest the opposite. The null hypothesis is that there is no tendency in either direction, hence that the numbers of positive and negative signs will be approximately equal. In that event, we would expect the value of W to approximate zero, within the limits of random variability.

For fairly small values of N, the properties of the sampling distribution of W can be figured out through simple (if tedious) enumeration of all the possibilities. Suppose, for example, that we had only N=3 subjects, whose absolute (unsigned) XA—XB differences produced the untied ranks 1, 2, and 3. The following table shows the possible combinations of plus and minus signs that could be distributed among these ranks, along with the value of W that each combination would produce.

 Ranks 
 1 
 2 
 3 
  W 
+
+
+
 +6 
—
+
+
 +4 
+
—
+
 +2 
+
+
—
 0 
—
—
+
 0 
—
+
—
 —2 
+
—
—
 —4 
—
—
—
 —6 


There is a total of 8 equally probable mere-chance combinations, of which exactly one would yield a positive value of W as large as +6, exactly two would yield a positive value as large as +4, and so on. And similarly at the other end of the distribution: exactly one combination yields a negative value of W as large as —6, exactly two yield negative values of W as large as —4, and so on. Hence the probability of ending up with a positive value of W as large as +4 is 2/8=.25; the probability of obtaining a negative value of W as large as —4 is 2/8=.25; and the "two-tailed" probability of finding a value of ±W as large as ±4 (in either direction) is (2/8)+(2/8)=.5.

The first of the following graphs shows the sampling distribution of this N=3 situation in pictorial form, and the other two show the corresponding distributions for the situations where N=4 and N=5. Note that for any such situation, the number of possible combinations of plus and minus signs is equal to 2N. Thus for N=3, 23=8; for N=4, 24=16; for N=5, 25=32, and so on.

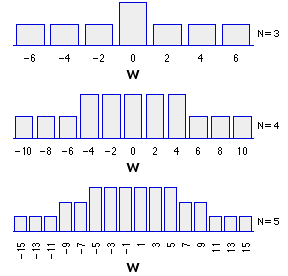
Examine the shapes of these distributions and you will surely see where things are heading. As the size of N increases, the sampling distribution of W comes closer and closer to the outlines of the normal distribution. With a sample of size N=10 or greater, the approximation is close enough to allow for the calculation of a z-ratio, which can then be referred to the unit normal distribution. (When N is smaller than 10, the observed value of W must be referred to an exact sampling distribution of the sort shown above for N=3, N=4, and N=5. A table of critical values of W for small sample sizes will be provided toward the end of this subchapter.)

We noted earlier that on the null hypothesis we would expect the value of W to approximate zero, within the limits of random variability. This is tantamount to saying that any particular observed value of W belongs to a sampling distribution whose mean is equal to zero. Hence

  -W = 0

Considerably less obvious is the standard deviation of the distribution. As it would be a distraction to try to make it obvious, I will resort to another of those "it can be shown" assertions and say simply: For any particular value of N, it can be shown that the standard deviation of the sampling distribution of W is equal to

-W = sqrt
[
N(N+1)(2N+1)
6
]

which for the present example, with N=14, works out as

-W = sqrt
[
14(14+1)(28+1)
6
]
= ±31.86

When considering the Mann-Whitney test in Subchapter 11a we noted that the z-ratio must include a "±.5" correction for continuity. The same is true for the Wilcoxon test, and for the same sort of reason. The measure designated as W can assume decimal values only as an artifact of the process of assigning tied ranks. Intrinsically, the absolute ranks—1, 2, 3, 4, etc.—on which W is based are all integers. Thus, the structure of the z-ratio for the Wilcoxon test is

z
=
(W—W)±.5
W

The correction for continuity is "—.5" when W is greater than -W and "+.5" when W is less than -W. Since -W is in all instances equal to zero, the simpler computational formula is

z
=
W—.5
W

For the present example, with N=14, W=67, and -W=±31.86, the result is

z
=
67—.5
31.86
= +2.09

From the following table of critical values of z, you can see that the observed value of z=+2.09 is significant just a shade beyond the .025 level for a directional test, which is the form of test called for by our investigator's directional hypothesis. For a two-tailed non-directional test, it would be significant just beyond the .05 level.

Critical Values of ±z
Level of Significance for a
Directional Test
.05 .025 .01 .005 .0005
Non-Directional Test
-- .05 .02 .01 .001
zcritical
  1.645     1.960     2.326     2.576     3.291  


When N is smaller than 10, the observed value of W must be referred to an exact sampling distribution of the sort described earlier. The following table shows the critical values of W for N=5 through N=9. For sample sizes smaller than N=5 there are no possible values of W that would be significant at or beyond the baseline .05 level.

Critical Values of ±W for Small Samples:
Level of Significance for a
Directional Test
.05 .025 .01 .005
Non-Directional Test
N -- .05 .02 .01
5   15     --     --     --  
6   17     21     --     --  
7   22     24     28     --  
8   26     30     34     36  
9   29     35     39     43  


The assumptions of the Wilcoxon test are:
  • that the paired values of XA and XB are randomly and independently drawn (i.e., each pair is drawn independently of all other pairs);T
  • that the dependent variable (e.g., a subject's probability estimate) is intrinsically continuous, capable in principle, if not in practice, of producing measures carried out to the nth decimal place; andT
  • that the measures of XA and XB have the properties of at least an ordinal scale of measurement, so that it is meaningful to speak of "greater than," "less than," and "equal to."

End of Subchapter 12a.
Return to Top of Subchapter 12a
Go to Chapter 13 [Conceptual Introduction to the Analysis of Variance]

Home Click this link only if the present page does not appear in a frameset headed by the logo Concepts and Applications of Inferential Statistics