In Chapter 11 we illustrated the independent-samples t-test with the example of an experiment aimed at determining whether two types of music have different effects on the performance of a mental task. Suppose that we were instead interested in assessing the relative effects of three types of music. In this case, the experimental procedure is the same in every detail, except that now we carry it out with three groups, one for each of the three types of music. As shown abstractly in the following table, what we end up with are three independent samples of measures, A, B, and C. If the three types of music have different effects on task performance, we would expect this fact to be reflected in significant differences among the means of the three samples.

A	B	C
Xa1 Xa2 Xa3 etc.	Xb1 Xb2 Xb3 etc.	Xc1 Xc2 Xc3 etc.
Ma	Mb	Mc

At first glance, you might suppose you could determine whether the three group means significantly differ form one another by performing a separate independent-samples t-test for each possible pair of means: that is,

	one test for Ma versus Mb
	another for Ma versus Mc
	and yet another for Mb versus Mc

A moment's reflection, however, will show why this simple strategy would not be advisable.

Essentially it is an exercise in disjunctive probabilities, along with a reminder of what it means to say than that some particular result is "significant." If an observed result is found to be significant at the basic .05 level, what this means is that there is only a 5% chance of its having occurred through mere chance. But 5% is still 5%! For any particular one of the three pair-wise t-test comparisons listed above, there would be a 5% probability by mere chance, even if the null hypothesis were true, of ending up with a difference that is "significant" at the .05 level. And three times 5% is 15%! If you were to perform all three of the pair-wise comparisons listed above, the disjunctive probability that one or another of them might end up "significant" at the .05 level by mere chance, absent any genuine differences among the effects of the three types of music, would be on the order of .05+.05+.05=.15. I say "on the order of" because the true disjunctive probability here would not be precisely .15, owing to some rather complex conditional probabilities that creep into situations of this sort. The main point, however, is independent of any particular numbers. If you are performing t-tests on multiple pairs of sample means, the probability that one or another of the comparisons might end up "significant" at the .05 level, by the merest chance, is substantially greater than .05.

The analysis of variance, commonly referred to by the acronym ANOVA, was first developed as a strategy for dealing with this sort of complication. At its lowest level it is essentially an extension of the logic of t-tests to those situations where we wish to compare the means of three or more samples concurrently. You will see in Chapter 16 that there are also higher, more complex levels to which the analysis of variance can ascend. But first the basics.

As its name suggests, the analysis of variance focuses on variability. It involves the calculation of several measures of variability, all of which come down to one or another version of the basic measure of variability introduced in Chapter 2, the sum of squared deviates. Before we get going, here is a brief reminder of how this "raw" measure of variability is obtained.

---

For any set of N values of X_i that derive from an equal-interval scale of measurement, a deviate is the difference between an individual value of X_i and the mean of the set:

deviate = X_i—M_X

a squared deviate is the square of that quantity:

squared deviate = (X_i—M_X)²

and the sum of squared deviates is the sum of all the squared deviates in the set:

SS = ∑(X_i—M_X)²

For practical computational purposes, it is often convenient to calculate the sum of squared deviates via the algebraically equivalent formula

SS = ∑X2i —

(∑Xi)2 iNi

---

¶The Logic of ANOVA

Here again is our scenario for three independent samples of measures, A, B, and C, except now we plug some specific numbers into the cells. Listed below the values of X_i in each of the three groups are five relevant summary statistics. I have also added a fourth column to include summary measures for the total array of data (all three groups combined). In each case, these latter summary measures are subscripted "T" for "Total." The sizes of the three groups separately are N_a=5, N_b=5, and N_c=5; hence N_T=15. The mean of all 15 of these combined values of X_i is M_T=18.2, and the sum of squared deviates of all 15 combined is SS_T=70.4.

	A	B	C	Total Array
	16 15 17 15 20	20 19 21 16 18	18 19 18 23 18	16 20 18 15 19 19 17 21 18 15 16 23 20 18 18
	Na=5 ∑Xai=83 ∑X2ai=1395 Ma=16.6 SSa=17.2	Nb=5 ∑Xbi=94 ∑X2bi=1782 Mb=18.8 SSb=14.8	Nc=5 ∑Xci=96 ∑X2ci=1862 Mc=19.2 SSc=18.8	NT=15 ∑XTi=273 ∑X2Ti=5039 MT=18.2 SST=70.4
	(If it is not clear where the four values of SS are coming from, click here for an account of the computational details.)

The Measure of Aggregate Differences among Sample Means

The central question here is: Do the means of the three samples significantly differ from one another?

Ma=16.6

Mb=18.8

Mc=19.2

So the first part of our task is to figure out a way of measuring the degree of their differences. If there were only two samples, the task would be quite easy: simply subtract the mean of one from the mean of the other. But that, of course, will not work when there are more than two samples. What you need in this more complex case is a measure of the aggregate degree to which the three (or more) group means differ. As it happens, there is a form of measurement you have already encountered that will perform this task quite handily. It is none other than that elemental "raw" measure of variability, the sum of squared deviates. The basic concept is that, whenever you have three or more numerical values, the measure of their variability is equivalent to the measure of their aggregate differences. That, indeed, is precisely what "variability" means: aggregate differences.

Here is how you could construct a sum of squared deviates measure for the three group means of the present example. For any particular group mean (the subscript "g" means "any particular group"), the deviate would be the difference between the group mean and M_T, the mean of the total array of data:

M_g—M_T

and the squared deviate would of course be the square of that quantity:

(M_g—M_T)²

The following table shows the numerical details of this procedure for each of the three groups.

	Ma=16.6	Mb=18.8	Mc=19.2		MT=18.2
	(16.6—18.2)2 2=2.56	(18.8—18.2)2 2=0.36	(19.2—18.2)2 2=1.0

These measures give you the squared deviates for each of the three group means, but they do not yet give you a sum of squared deviates. Actually, what we will now end up with is not so much a sum as a weighting. That is, we will be weighting (adding weight) to the squared deviate of each of the group means in accordance with the number of individual values of X_i on which the group mean is based: N_a=5 for group A, N_b=5 for group B, and N_c=5 for group C. Thus, for any particular group mean, the squared deviate is

(M_g—M_T)²

and the corresponding "sum" of squared deviates is the squared deviate multiplied by the appropriate value of N

N_g(M_g—M_T)²

Here again are the numerical details.

	Na=5 Ma=16.6	Nb=5 Mb=18.8	Nc=5 Mc=19.2		MT=18.2
	5(16.6—18.2)2 2=12.8	5(18.8—18.2)2 2=1.8	5(19.2—18.2)2 2=5.0

The sum of these three resulting values, 12.8+1.8+5.0=19.6, will give you a quantity spoken of within the context of the analysis of variance as the sum of squared deviates between-groups, rendered symbolically as SS_bg. And that is our aggregate measure of the degree to which the three sample means differ from one another: SS_bg=19.6.

The Measure of Background Random Variability

Once we have this measure, all that remains is to figure a way to determine whether it differs significantly from the zero that would be specified by the null hypothesis. As a first step, return for a moment to the formula for the independent-samples t-test:

t

=

MXa—MXb est.iM—M

Formula for independent-samples t-test, from Ch. 11.

Clearly our measure of SS_bg is analogous to the numerator of this formula: M_Xa—M_Xb is the difference between two means; SS_bg is the difference among three or more means. What we now need to find is an appropriate analogy for the denominator. The way to find it is to look behind the abstract notation, i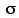_M—M, to see the more general concept that it embodies.

What it refers to in the first instance, of course, is that elaborate mouthful, "the standard deviation of the sampling distribution of sample-mean differences." More generally, you can say it refers to "the standard deviation of the sampling distribution that happens to be appropriate in this particular situation." And even more generally, you can say it refers to "the measure of sheer, cussed random variability that happens to pertain to this particular situation." Whenever you perform a test of statistical significance, what you are essentially doing is comparing an observed fact to a measure of the random variability in which it is embedded; the aim of the comparison is to determine whether the fact—in this case, the aggregate difference among the three sample means—goes beyond anything that mere random variability might have produced.

In the independent-samples t-test, the ultimate source of your measure of random variability is the variability that appears inside each of the two samples, A and B, as measured by SS_a and SS_b. The same is true when you have more than two samples. In our original table of data we observed the following values of SS for our three samples, A, B, and C:

SSa=17.2

SSb=14.8

SSc=18.8

Taken together, they constitute a quantity known as sum of squared deviates within-groups, symbolized as SS_wg. Thus,

	SSwg	= SSa+SSb+SSc
		= 17.2+14.8+18.8
		= 50.8

So here is where we stand up to this point: SS_bg=19.6 is the aggregate raw measure of the degree to which our three sample means differ, and SS_wg=50.8 is the raw measure of the random variability in which these sample-mean differences are embedded. I say "raw" in both cases, because each of these measures will have to be refined somewhat before we can actually use them. But more of that in a moment. First I want to call your attention to a remarkable connectedness among the various numbers that you have been scrolling through in this chapter. At the very top came SS_T=70.4, the measure of variability within the entire array of data for all three groups combined. Then came SS_bg=19.6, then SS_wg=50.8. Add the latter two together and the result is the same 70.4 that was found for SS_T. The correspondence is no accident. When SS_T, SS_bg, and SS_wg are calculated in the manner just described, it is always and necessarily the case that SS_bg and SS_wg add up to SS_T (within the limits of rounding error). It is hardly surprising. SS_T is the total variability of the array, and there are only two places where portions of that total can be distributed: either within the groups or between the groups. The relationships among these three measures of variability are described by the following identities:

	SST = SSwg + SSbg
	SSbg = SST — SSwg
	SSwg = SST — SSbg

The Refinement of Between-Groups and Within-Groups Measures

In Chapters 9 through 12 you encountered several versions of the basic concept that the variance of a source population can be estimated as

est.2source =

sum of squared deviates degrees of freedom

You have also seen in previous chapters that the basic concept of degrees of freedom in this context is "N—1," where "N" refers to the number of items on which the measure of sum of squared deviates is based. Using these same concepts, we now proceed to form two separate estimates of source population variance, one on the basis of SS_bg and the other on the basis of SS_wg. I will first go through the mechanics of the process, and then come back to try to explain just what it is that these variance estimates are aiming to estimate.

Within the context of the analysis of variance, an estimate of a source population variance is spoken of as a mean square (shorthand for "mean of the squared deviates") and conventionally symbolized as MS. The value of the between-groups SS in this example is based on the means of three groups, so the number of degrees of freedom associated with SS_bg is df_bg=3—1=2, and the variance estimate is

MS_bg = SS_bg / df_bg

MS_bg = 19.6 / 2 = 9.8

The value of the within-groups SS is the sum of the separate SS measures for each of the three samples: SS_a, SS_b, and SS_c. Each of these separate within-groups measures of SS is associated with a certain number of degrees of freedom: N_a—1, N_b—1, and N_c—1, respectively. So the number of degrees of freedom associated with the composite within-groups measure, SS_wg, is

(N_a—1)+(N_b—1)+(N_c—1)

which in the present case comes out to df_wg=12. So here the variance estimate is

MS_wg = SS_wg / df_wg

MS_wg = 50.8 / 12 = 4.23

Now back to the question of just what it is that these two variance estimates, MS_bg=9.8 and MS_wg=4.23, are aiming to estimate. The simplest answer is that they are both estimates of the same thing. In the general case where you have three (or more) independent samples of measures arrayed in the fashion shown abstractly at the beginning of this chapter,

A	B	C
Xa1 Xa2 Xa3 etc.	Xb1 Xb2 Xb3 etc.	Xc1 Xc2 Xc3 etc.
Ma	Mb	Mc

the null hypothesis is that the values of X_i in the three samples have all been drawn indifferently from the same underlying source population. Our two values of MS, for between-groups and within-groups, are both estimates of the variance of the population assumed by the null hypothesis to be the common source of all three samples. The relationship between these two estimates is rather complicated, and we will not try to go into it in fine-grained detail. Suffice it to say that

• when the null hypothesis is true, MS_bg will tend to be equal to or less than MS_wg; and
• when^xthe null hypothesis is not true, MS_bg will tend to be greater than MS_wg

  ---

  To understand why the latter is so, recall that MS_bg reflects the aggregate degree of difference among the means of the several samples, while MS_wg is a measure of the amount of random variability that exists inside the groups. When the null hypothesis is false, the means of the groups will tend to differ substantially from one another, and the value of MS_bg will increase accordingly. At the same time, the relative size of MS_wg will decrease.

  ---

The F-Ratio

The relationship between two values of MS is conventionally described by a ratio known as F, which is defined for the general case as

F =

MSeffect MSerror

where MS_effect is a variance estimate pertaining to the particular fact whose significance you wish to assess (e.g., the differences among the means of several independent samples), and MS_error is a variance estimate reflecting the amount of sheer, cussed random variability that is present in the situation. For the present example, MS_effect would be the same as MS_bg and MS_error would be the same as MS_wg. When the null hypothesis is true, the F-ratio will tend to be equal to or less than 1.0, within the limits of random variability; and when the null hypothesis is false, the F-ratio will tend to be significantly greater than 1.0. In the present example, the ratio comes out as

F =

=

MSbg MSwg

=

9.8 4.23

= 2.32

You will certainly be able to anticipate what comes next. Granted that F=2.32 is greater than the null hypothesis stipulation of F<1.0: How likely is it that a difference this large or larger might have occurred through mere chance coincidence? Same song, new verse. As with z, t, and chi-square, the destiny of a calculated F-ratio is to be referred to its appropriate sampling distribution.

Before we get into the theoretical details of this point, here is an exercise that will allow you to simulate the sampling distribution of F that applies to this particular example. In Chapter 9 we defined a normally distributed reference population that has a mean of 18 and a standard deviation of ±3. Each time you click the button below, labeled "Samples," your computer will draw three random samples of X_i from this common source population, each sample of size N=5. As the null hypothesis in this case is patently true for each set of samples, you would expect most of the resulting F-ratios to be equal to or less than 1.0; though of course some will be greater than 1.0, perhaps even substantially greater, through sheer, cussed random variability.

Click the button repeatedly and try to get a sense of how often these mere-chance F-ratios come out equal to or greater than our calculated value of 2.32. If the proportion of such cases over the long run is 5% or less, then F=2.32 can be regarded as significant at or beyond the basic .05 level. If it is more than 5%, then F=2.32 is non-significant. The cell labeled "PCT" will perform a running calculation of the percentage of cases in which the mere-chance F-ratio is equal to or greater than 2.32. If you continue clicking the button long enough (at least 50 times, preferably several hundred), you will see this percentage beginning to settle in at about 14%, which is of course quite a lot larger than the 5% or less that you are looking for. So our calculated value of 2.32 is, in a word, non-significant. In a situation of this particular type—three independent samples, each of size N=5—an F-ratio this large or larger could readily occur by mere chance.

---

	A	B	C
				MT=; SST= SSbg=; MSbg= SSwg=; MSwg= F=; PCT=%
Mg
SSg

---

¶The Sampling Distributions of F

You have already seen that for values of z there is only one sampling distribution, whereas for t and chi-square there is in principle a different sampling distribution for each possible value of df, degrees of freedom. With F the situation becomes even more complex, for here there are two distinct values of df to be taken into account: one pertaining to the numerator of the ratio and the other pertaining to the denominator. Recall that when you calculate an F-ratio of the general form

F =

=

MSbg MSwg

what you are actually calculating is

F =

=

MSbg MSwg

=

SSbg / dfbg SSwg / dfwg

Hence the numerator of the F-ratio is associated with df_bg, the denominator with df_wg. For the present example, df_bg=2 and df_wg=12, so the F-ratio in this case is associated with 2 and 12 degrees of freedom for the numerator and denominator, respectively. The conventional notation for a pairing of numerator/denominator df values of this type is "df=2,12."

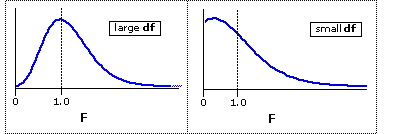
There is a separate sampling distribution of F for each possible pair of such numerator/denominator df values. Thus, there is one sampling distribution for df=2,12, another for df=2,15, another for df=12,160, and so on. The shapes of these various sampling distributions lie within the range of the two extreme forms shown below in Figure 13.1. With quite large values of df, the highest point of the curve will tend to be reached at F=1.0, while with smaller values of df it will fall somewhere to the left of F=1.0. In all cases, however, the portion of the curve that falls to the right of F=1.0 has much the same shape: the curve drops steeply at first, and then more gradually.

Figure 13.1. The Sampling Distributions of F



The next figure shows the sampling distribution of F that applies to the example described above, where the df values for numerator and denominator are 2 and 12. For the sake of simplicity, the horizontal axis in this graph begins at F=1.0. The stippled blue patch is just a reminder that a portion of the distribution lies invisibly to the left of 1.0.

Figure 13.2. Sampling Distribution of F for df=2,12



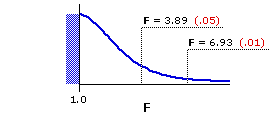
As indicated by the accompanying notations, F=3.89 and F=6.93 mark the points beyond which fall 5% and 1%, respectively, of all possible mere-chance outcomes, assuming the null hypothesis to be true. An observed F-ratio equal to or greater than 3.89 would therefore be significant at or beyond the .05 level, while one equal to or greater than 6.93 would be significant at or beyond the .01 level.

Because of the very large number of separate sampling distributions, tables of critical values for F typically list only the values for the .05 level and the .01 level. The following abridged table will give you an idea of how it is all laid out. Across the top are values of df for the numerator of the F-ratio, and down the side on the left are df values for the denominator. For each combination of df_numerator and df_denominator, the critical value for the .05 level is listed in plain type, while the critical value for the .01 level is given in bold-face type. Thus, for df=2,12 the listings appear as "3.89" and "6.93." For df=4,10, it is "3.48" and "5.99." And so on. A more complete table of critical values of F is found in Appendix D.

df denominator	df numerator
	1	2	3	4
10	4.96 10.04	4.10 7.56	3.71 6.55	3.48 5.99
11	4.84 9.65	3.98 7.21	3.59 6.22	3.36 5.67
12	4.75 9.33	3.89 6.93	3.49 5.95	3.26 5.41
13	4.67 9.07	3.81 6.70	3.41 5.74	3.18 5.20

---

¶The Relationship Between F and t

Although it is not normally done this way, the analysis of variance can also be applied to situations where you have only two groups of measures—in particular, to situations of the sort described in Chapters 11 and 12 in connection with t-tests for independent samples and correlated samples. And when you do apply it to two-sample situations of this type, the results are equivalent to what would be found in the corresponding t-test. Within the limits of rounding errors, the F-ratio obtained in such an analysis will be equal to the square of the corresponding t-ratio. The only difference is that a t-test can be either directional or non-directional, whereas the analysis of variance is (like chi-square) intrinsically non-directional. [Click here if you would like to see the equivalence of t and F in the two-sample case illustrated with a specific example.]

---

¶Applications of F

Of course, if you had only two groups you would not really want to bother with the apparatus of the F-ratio, because you could arrive at the same place more easily with a simple t-test. The advantage of the F-ratio is that its logic and procedure, once developed, can then be extended to those numerous cases where the researcher might wish to examine three or more samples concurrently.

The simplest application, introduced in the present chapter and covered more fully in Chapter 14, is for the case where you have three or more independent samples. The procedure for three or more correlated samples covered in Chapter 15 is a bit more complex, although its obvious analogy with the correlated-samples t-test will smooth the path considerably. Both of these relatively simple applications fall under the heading of one-way analysis of variance, so named because they can consider only one independent variable at a time—type of music (A, B, C), loudness of a particular type of music (low, medium, high), type of drug (X, Y, Z), dosage of a particular type of drug (0mg, 5mg, 10mg), and so on.

Considerably more complex, though at the same time far more useful, is the two-way analysis of variance introduced in Chapter 16. As its name suggests, this is a procedure that allows you to examine the effects of two independent variables concurrently; for example, the effects of two different drugs, A and B, each at three different dosage levels, 0mg, 5mg, and 10mg. Here the levels of drug A would constitute one independent variable, the levels of drug B would constitute another. This two-way version of the analysis of variance would not only allow you to test the two drugs concurrently; it would also potentially be able to tell you whether the two drugs interact. I introduce this concept with the example of two drugs only because that is a form of interaction you have no doubt already heard about or read about, or perhaps even experienced at first hand, for better or worse. The possibility of two variables interacting, however, is by no means limited to the realm of drugs. There are many precincts of science where the disentangling of interaction effects is one of the main challenges of the enterprise. This is especially so within the domains of the biological and behavioral sciences.

Whether simple or complex, however, all analysis of variance procedures end up with the calculation of one or more F-ratios of the general form described above:

F =

MSeffect MSerror

where MS_effect is a measure pertaining to the particular fact whose significance you wish to assess, and MS_error is a variance estimate reflecting the amount of sheer, cussed random variability that is present in the situation. Once again: same song, new verse. It is all cut from the same pattern you have seen building up since about Chapter 6.

This chapter includes an Appendix that will generate a graphic and numerical display of the properties of the sampling distribution of F for any value of dfnumerator and for values of dfdenominator >5. As the page opens, you will be prompted for the two values of df.