©Richard Lowry, 1999-
All rights reserved.
Chapter 11.
t-Test for the Significance of the Difference between the Means of Two Independent Samples
This is probably the most widely used statistical test of all time, and certainly the most widely known. It is simple, straightforward, easy to use, and adaptable to a broad range of situations. No statistical toolbox should ever be without it.
Its utility is occasioned by the fact that scientific research very often examines the phenomena of nature two variables at a time, with an eye toward answering the basic question: Are these two variables related? If we alter the level of one, will we thereby alter the level of the other? Or alternatively: If we examine two different levels of one variable, will we find them to be associated with different levels of the other?
Here are three examples to give you an idea of how these abstractions might find expression in concrete reality. On the left of each row of cells is a specific research question, and on the right is a brief account of a strategy that might be used to answer it. The first two examples illustrate a very frequently employed form of experimental design that involves randomly sorting the members of a subject pool into two separate groups, treating the two groups differently with respect to a certain independent variable, and then measuring both groups on a certain dependent variable with the aim of determining whether the differential treatment produces differential effects. (Variables: Independent and Dependent.) A quasi-experimental variation on this theme, illustrated by the third example, involves randomly selecting two groups of subjects that already differ with respect to one variable, and then measuring both groups on another variable to determine whether the different levels of the first are associated with different levels of the second.
In each of these cases, the two samples are independent of each other in the obvious sense that they are separate samples containing different sets of individual subjects. The individual measures in group A are in no way linked with or related to any of the individual measures in group B, and vice versa. The version of a t-test examined in this chapter will assess the significance of the difference between the means of two such samples, providing: (i) that the two samples are randomly drawn from normally distributed populations; and (ii) that the measures of which the two samples are composed are equal-interval.
To illustrate the procedures for this version of at-test, imagine we were actually to conduct the experiment described in the second of the above examples. We begin with a fairly homogeneous subject pool of 30 college students, randomly sorting them into two groups, A and B, of sizes Na=15 and Nb=15. (It is not essential for this procedure that the two samples be of the same size.) We then have the members of each group, one at a time, perform a series of 40 mental tasks while one or the other of the music types is playing in the background. For the members of group A it is music of type-I, while for those of group B it is music of type-II. The following table shows how many of the 40 components of the series each subject was able to complete. Also shown are the means and sums of squared deviates for the two groups.
¶Null Hypothesis
Recall from Chapter 7 that whenever you perform a statistical test, what you are testing, fundamentally, is the null hypothesis. In general, the null hypothesis is the logical antithesis of whatever hypothesis it is that the investigator is seeking to examine. For the present example, the research hypothesis is that the two types of music have different effects, so the null hypothesis is that they do not have different effects. Its immediate implication is that any difference we find between the means of the two samples should not significantly differ from zero.
If the investigator specifies the direction of the difference in advance as either
then the research hypothesis is directional and permits a one-tail test of significance. A non-directional research hypothesis would require a two-tail test, as it is the equivalent of saying "I'm expecting a difference in one direction or the other, but I can't guess which." For the sake of discussion, let us suppose we had started out with the directional hypothesis that task performance will be better with type-I music than with type-II music. Clearly our observed result, Ma—Mb=2.26, is in the hypothesized direction. All that remains is to determine how confident we can be that it comes from anything more than mere chance coincidence.
¶Logic and Procedure
The groundwork for the following points is laid down in Chapter 9.
¶Inference
Figure 11.1 shows the sampling distribution of tfor df=28. Also shown is the portion of the table of critical values of t (Appendix C) that pertains to df=28. The designation "tobs" refers to our observed value of t=+1.9. We started out with the directional research hypothesis that task performance would be better for group A than for group B, and as our observed result, MXa—MXb=2.26, proved consistent with that hypothesis, the relevant critical values of t are those that pertain to a directional (one-tail) test of significance: 1.70 for the .05 level of significance, 2.05 for the .025 level, 2.47 for the .01 level, and so on.
Figure 11.1. Sampling Distribution of t for df=28
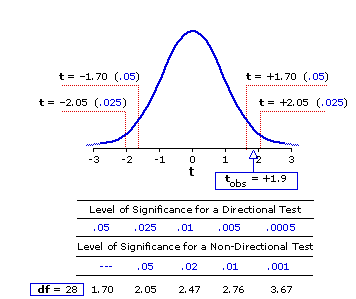
If our observed value of t had ended up smaller than 1.70, the result of the experiment would be non-significant vis-à-vis the conventional criterion that the mere-chance probability of a result must be equal to or less than .05. If it had come out at precisely 1.70, we would conclude that the result is significant at the .05 level. As it happens, the observed t meets and somewhat exceeds the 1.70 critical value, so we conclude that our result is significant somewhat beyond the .05 level. If the observed t had been equal to or greater than 2.05, we would have been able to regard the result as significant at or beyond the .025 level; and so on.
The same logic would have applied to the left tail of the distribution if our initial research hypothesis had been in the opposite direction, stipulating that task performance would be better with music of type-II than with music of type-I. In this case we would have expected MXa to be smaller than MXb, which would have entailed a negative sign for the resulting value of t.
If, on the other hand, we had begun with no directional hypothesis at all, we would in effect have been expecting
either MXa>MXb or MXa<MXb
and that disjunctive expectation ("either the one or the other") would have required a non-directional, two-tailed test. Note that for a non-directional test our observed value oft=+1.9 (actually, for a two-tailed test it would have to be regarded as t=±1.9) would not be significant at the minimal .05 level. (The distinction between directional and non-directional tests of significance is introduced in Chapter 7.)
In this particular case, however, we did begin with a directional hypothesis, and the obtained result as assessed by a directional test is significant beyond the .05 level. The practical, bottom-line meaning of this conclusion is that the likelihood of our experimental result having come about through mere random variability—mere chance coincidence, "sampling error," the luck of the scientific draw—is a somewhat less that 5%; hence, we can have about 95% confidence that the observed result reflects something more than mere random variability. For the present example, this "something more" would presumably be a genuine difference between the effects of the two types of music on the performance of this particular type of task.
¶Step-by-Step Computational Procedure: t-Test for the Significance of the Difference between the Means of Two independent Samples
Step 2. Estimate the variance of the source population as
Step 3. Estimate the standard deviation of the sampling distribution of sample-mean differences (the "standard error" of MXa—MXb) as
Step 4. Calculate t as
Step 5. Refer the calculated value of t to the table of critical values of t (Appendix C), withdf=(Na—1)+(Nb—1). Keep in mind that a one-tailed directional test can be applied only if a specific directional hypothesis has been stipulated in advance; otherwise it must be a non-directional two-tailed test.
Note that this chapter includes a subchapter on the Mann-Whitney Test, which is a non-parametric alternative to the independent-samples t-test.
Its utility is occasioned by the fact that scientific research very often examines the phenomena of nature two variables at a time, with an eye toward answering the basic question: Are these two variables related? If we alter the level of one, will we thereby alter the level of the other? Or alternatively: If we examine two different levels of one variable, will we find them to be associated with different levels of the other?
Here are three examples to give you an idea of how these abstractions might find expression in concrete reality. On the left of each row of cells is a specific research question, and on the right is a brief account of a strategy that might be used to answer it. The first two examples illustrate a very frequently employed form of experimental design that involves randomly sorting the members of a subject pool into two separate groups, treating the two groups differently with respect to a certain independent variable, and then measuring both groups on a certain dependent variable with the aim of determining whether the differential treatment produces differential effects. (Variables: Independent and Dependent.) A quasi-experimental variation on this theme, illustrated by the third example, involves randomly selecting two groups of subjects that already differ with respect to one variable, and then measuring both groups on another variable to determine whether the different levels of the first are associated with different levels of the second.
| Question | Strategy
| Does the presence of a certain kind of mycorrhizal fungus enhance the growth of a certain kind of plant?
| Begin with a "subject pool" of seeds of the type of plant in question. Randomly sort them into two groups, A and B. Plant and grow them under conditions that are identical in every respect except one: namely, that the seeds of group A (the experimental group) are grown in a soil that contains the fungus, while those of group B (the control group) are grown in a soil that does not contain the fungus. After some specified period of time, harvest the plants of both groups and take the relevant measure of their respective degrees of growth. If the presence of the fungus does enhance growth, the average measure should prove greater for group A than for group B.
| Do two types of music, | Begin with a subject pool of college students, relatively homogeneous with respect to age, record of academic achievement, and other variables potentially relevant to the performance of such a task. Randomly sort the subjects into two groups, A and B. Have the members of each group perform the series of mental tasks under conditions that are identical in every respect except one: namely, that group A has music of | Do two strains of mice, A and B, differ with respect to their ability to learn to avoid an aversive stimulus?
| With this type of situation you are in effect starting out with two subject pools, one for strain A and one for strain B. Draw a random sample of size Na from pool A and another of size Nb from pool B. Run the members of each group through a standard aversive-conditioning procedure, measuring for each one how well and quickly the avoidance behavior is acquired. Any difference between the avoidance-learning abilities of the two strains should manifest itself as a difference between their respective group means.
| |
In each of these cases, the two samples are independent of each other in the obvious sense that they are separate samples containing different sets of individual subjects. The individual measures in group A are in no way linked with or related to any of the individual measures in group B, and vice versa. The version of a t-test examined in this chapter will assess the significance of the difference between the means of two such samples, providing: (i) that the two samples are randomly drawn from normally distributed populations; and (ii) that the measures of which the two samples are composed are equal-interval.
To illustrate the procedures for this version of a
Group A
music of type-IGroup B
music of type-II26 21 22
26 19 22
26 25 24
21 23 23
18 29 22
18 23 21
20 20 29
20 16 20
26 21 25
17 18 19
Na=15
Ma=23.13
SSa=119.73Nb=15
Mb=20.87
SSb=175.73Ma—Mb=2.26
¶Null Hypothesis
Recall from Chapter 7 that whenever you perform a statistical test, what you are testing, fundamentally, is the null hypothesis. In general, the null hypothesis is the logical antithesis of whatever hypothesis it is that the investigator is seeking to examine. For the present example, the research hypothesis is that the two types of music have different effects, so the null hypothesis is that they do not have different effects. Its immediate implication is that any difference we find between the means of the two samples should not significantly differ from zero.
If the investigator specifies the direction of the difference in advance as either
task performance will be better with type-I music than with type-II | which would be supported by finding the mean of sample A to be significantly greater than the mean of sample B (Ma>Mb) or
|
| task performance will be better with type-II music than with type-I which would be supported by finding the mean of sample B to be significantly greater than the mean of sample A (Mb>Ma) |
¶Logic and Procedure
The groundwork for the following points is laid down in Chapter 9.
| (1) | The mean of a sample randomly drawn from a normally distributed source population belongs to a sampling distribution of sample means that is also normal in form. The overall mean of this sampling distribution will be identical with the mean of the source population: |
|
i | From Ch.9, Pt.1 |
| (2) |
For two samples, each randomly drawn from a normally distributed source population, the difference between the means of the two samples,
belongs to a sampling distribution that is normal in form, with an overall mean equal to the difference between the means of the two source populations | |
|
i | From Ch.9, Pt.1 |
| (2) |
On the null hypothesis, i | |
|
i |
| (3) | For the present example, the null hypothesis holds that the two types of music do not have differential effects on task performance. This is tantamount to saying that the measures of task performance in groups A and B are all drawn indifferently from the same source population of such measures. In items 3 and 4 below, the phrase "source population" is a shorthand way of saying "the population of measures that the null hypothesis assumes to have been the common source of the measures in both groups."
| (3)
| If we knew the variance of the source population, we would then be able to calculate the standard deviation (aka "standard error") of the sampling distribution of sample-mean differences as
| |
| x | [ | x Na | + | x Nb | ] | From Ch.9, Pt.1 |
| (3) | This, in turn, would allow us to test the null hypothesis for any particular Ma—Mb difference by calculating the appropriate z-ratio |
| z = | MXa—MXb | From Ch.9, Pt.1 |
| (3) | and referring the result to the unit normal distribution.
In most practical research situations, however, the variance of the source population, hence also the value of |
| t | = | MXa—MXb est.i | From Ch.9, Pt.2 |
| (3) | The resulting value belongs to the particular sampling distribution of t that is defined by df=(Na—1)+(Nb—1). |
| (4) | To help you keep track of where the particular numerical values are coming from beyond this point, here again are the summary statistics for our hypothetical experiment on the effects of two types of music: |
Group A
music of type-IGroup B
music of type-IINa=15
Ma=23.13
SSa=119.73Nb=15
Mb=20.86
SSb=175.73Ma—Mb=2.26
| (3) | As indicated in Chapter 9, the variance of the source population can be estimated as |
| {s2p} | = | SSa+SSb (Na—1)+(Nb—1) | From Ch.9, Pt.2 |
| (3) | which for the present example comes out as |
| {s2p} | = | 119.73+175.73 14+14 | = 10.55 |
| (3) | This, in turn, allows us to estimate the standard deviation of the sampling distribution of sample-mean differences as |
| = sqrt | [ | {s2p} Na | + | {s2p} Nb | ] | From Ch.9, Pt.2
|
| = sqrt | [ | 10.55 | 15 + | 10.55 | 15 ] | = ±1.19 | |
| (4) | And with this estimated value of |
| t | = | MXa—MXb est.i
|
| = | 23.13—20.87 | 1.19 = +1.9 | |
| (4) | with df=(15—1)+(15—1)=28 In the calculation of a two-sample t-ratio, note that the sign of t depends on the direction of the difference between MXa and MXb. MXa>MXb will produce a positive value of t, while MXa<MXb will produce a negative value of t. |
¶Inference
Figure 11.1 shows the sampling distribution of t
Figure 11.1. Sampling Distribution of t for df=28

If our observed value of t had ended up smaller than 1.70, the result of the experiment would be non-significant vis-à-vis the conventional criterion that the mere-chance probability of a result must be equal to or less than .05. If it had come out at precisely 1.70, we would conclude that the result is significant at the .05 level. As it happens, the observed t meets and somewhat exceeds the 1.70 critical value, so we conclude that our result is significant somewhat beyond the .05 level. If the observed t had been equal to or greater than 2.05, we would have been able to regard the result as significant at or beyond the .025 level; and so on.
The same logic would have applied to the left tail of the distribution if our initial research hypothesis had been in the opposite direction, stipulating that task performance would be better with music of type-II than with music of type-I. In this case we would have expected MXa to be smaller than MXb, which would have entailed a negative sign for the resulting value of t.
If, on the other hand, we had begun with no directional hypothesis at all, we would in effect have been expecting
and that disjunctive expectation ("either the one or the other") would have required a non-directional, two-tailed test. Note that for a non-directional test our observed value of
In this particular case, however, we did begin with a directional hypothesis, and the obtained result as assessed by a directional test is significant beyond the .05 level. The practical, bottom-line meaning of this conclusion is that the likelihood of our experimental result having come about through mere random variability—
¶Step-by-Step Computational Procedure: t-Test for the Significance of the Difference between the Means of Two independent Samples
Note that this test makes the following assumptions and can be meaningfully applied only insofar as these assumptions are met:
That the two samples are independently and randomly drawn from the source population(s).
That the scale of measurement for both samples has the properties of an equal interval scale.
That the source population(s) can be reasonably supposed to have a normal distribution.
Step 1. For the two samples, A and B, of sizes of Na and Nb respectively, calculate| MXa and SSa | the mean and sum of squared deviates of sample A
| MXb and SSb
|
| the mean and sum of squared deviates of sample B |
Step 2. Estimate the variance of the source population as
| {s2p} | = | SSa+SSb (Na—1)+(Nb—1) |
Recall that "source population" in this context means "the population of measures that the null hypothesis assumes to have been the common source of the measures in both groups."
Step 3. Estimate the standard deviation of the sampling distribution of sample-mean differences (the "standard error" of MXa—MXb) as
| est.i | [ | {s2p} Na | + | {s2p} Nb | ] |
Step 4. Calculate t as
| t | = | MXa—MXb est.i |
Step 5. Refer the calculated value of t to the table of critical values of t (Appendix C), with
Note that this chapter includes a subchapter on the Mann-Whitney Test, which is a non-
End of Chapter 11.
Return to Top of Chapter 11
Go to Subchapter 11a [Mann-
Go to Chapter 12 [t-Test for Two Correlated Samples]
| Home | Click this link only if the present page does not appear in a frameset headed by the logo Concepts and Applications of Inferential Statistics |