©Richard Lowry, 1999-
All rights reserved.

Subchapter 11a.
The Mann-Whitney Test

Twenty-one persons seeking treatment for claustrophobia are independently and randomly sorted into two groups, the first of size na=11 and the second of size nb=10. The members of the first group each individually receive Treatment A over a period of 15 weeks, while those of the second group receive Treatment B. The investigators' directional hypothesis is that Treatment A will prove the more effective.

At the end of the experimental treatment period, the subjects are individually placed in a series of claustrophobia test situations, knowing that their reactions to these situations are being recorded on videotape. Subsequently three clinical experts, uninvolved in the experimental treatment and not knowing which subject received which treatment, independently view the videotapes and rate each subject according to the degree of claustrophobic tendency shown in the test situations. Each judge's rating takes place along a 10-point scale, with 1="very low" and 10="very high"; and the final measure for each subject is the simple average of the ratings of the three judges for that subject. The following table shows the average ratings for each subject in each of the two groups.

Group A
Group B
  4.64.74.9  
  5.15.25.5  
  5.86.16.5  
  6.57.2
  5.25.35.4  
  5.66.26.3  
  6.87.78.0  
  8.1
mean
5.6
6.5

The investigators expected Treatment A to prove the more effective, and sure enough it is group A that appears to show the lower mean level of claustrophobic tendency in the test situations. You might suppose that all they need do now is plug their data into an independent-samples t-test to see whether the observed mean difference is significant.

If you ever find yourself with a set of data of this sort, and are seized by the impulse to plug the numbers into a t-test, please lie down until the impulse passes. For the fact is that a t-test could not legitimately be used in this particular situation, nor in any other where the assumptions of the test are so patently violated. As indicated in the main body of Chapter 11, the t-test for independent samples can be meaningfully applied only insofar as
  1. the two samples are independently and randomly drawn from the source population(s);T
  2. the scale of measurement for both samples has the properties of an equal interval scale; andT
  3. the source population(s) can be reasonably supposed to have a normal distribution.
While our initial sorting of the subjects into groups A and B satisfies the first requirement in the list, the second and third requirements are clearly not met. A rating scale cannot be assumed to possess the properties of an equal interval scale. Moreover, as you can see from the adjacent graph, there is nothing in the data to suggest an underlying normal distribution. The indication, indeed, is that the distribution of the underlying population might have a rather pronounced positive skew. (The graph shows the frequency distribution for the 21 subjects of both groups combined, sorted into the intervals 4.5 to 5.4, 5.5 to 6.4, 6.5 to 7.4, and 7.5 to 8.4.)

The admonition to refrain from using a t-test in situations of this sort is not simply a matter of good manners or good taste. The t-test makes these particular assumptions about the data you are feeding into it. Feed it the type of information it assumes it is getting, and the result it gives you in return will provide a firm basis for drawing rational conclusions. Feed it information that violates any one or several of its assumptions, and it will still patiently crunch the numbers and crank out a result. But that result will be nonsense, and so too will be any conclusion you might draw from it. The "significant" result that would come from applying a t-test to this set of data would in fact be no result at all. It would be merely the semblance of a result.

Assumption 2, an equal-interval scale of measurement; assumption 3, an underlying normal distribution. In cases where data from two independent samples fail to meet either or both of these requirements, one is well advised to forego the t-test and turn instead to its non-parametric alternative, the Mann-Whitney Test. The only assumptions of the Mann-Whitney test are
  1. that the two samples are randomly and independently drawn;T
  2. that the dependent variable (e.g., claustrophobic tendency) is intrinsically continuous, capable in principle, if not in practice, of producing measures carried out to the nth decimal place; andT
  3. that the measures within the two samples have the properties of at least an ordinal scale of measurement, so that it is meaningful to speak of "greater than," "less than," and "equal to."
We will begin with the sheer mechanics of the Mann-Whitney procedure, and then come back to consider its underlying logic. Actually, there are two separate sequences in the logic of the Mann-Whitney test. The first, described here as Method I, is the more widely applicable. The second, Method II, is needed only when one or another of the samples is fairly tiny.

¶Mechanics

It begins by assembling the measures from samples A and B into a single set of size N=na+nb. These measures are then rank-ordered from lowest (rank#1) to highest (rank#N), with tied ranks included where appropriate. For the present set of data, this process would yield the following result.

Raw
Measure
Rank from
Sample
4.6
4.7
4.9
5.1
5.2
5.2
5.3
5.4
5.5
5.6
5.8
6.1
6.2
6.3
6.5
6.5
6.8
7.2
7.7
8.0
8.1
1
2
3
4
5.5
5.5
7
8
9
10
11
12
13
14
15.5
15.5
17
18
19
20
21
A
A
A
A
A
B
B
B
A
B
A
A
B
B
A
A
B
A
B
B
B


N
= na + nb
= 11 + 10 = 21


Tied Ranks. Note that two of the entries in the raw-measures column each have the value of 5.2. As these two entries fall in the sequence where ranks #5 and #6 would be, in the absence of such a tie, they are each given the average of these two ranks, which is 5.5. Similarly for the two raw-measure entries whose value is 6.5; each is accorded the average of ranks #15 and #16, which is 15.5. If there were three raw-measure entries tied for ranks 8, 9, and 10, each would receive the average of those ranks, which is 9. And so on.


Once they have been sorted out in this fashion, the rankings are then returned to the sample, A or B, to which they belong and substituted for the raw measures that gave rise to them. Thus, the raw measures that appear in the following table on the left are replaced by their respective ranks, as shown in the table on the right.


Raw Measures
 Ranked Measures
Group A
Group B
Group A
Group B
4.6
4.7
4.9
5.1
5.2
5.5
5.8
6.1
6.5
6.5
7.2
 		5.2
5.3
5.4
5.6
6.2
6.3
6.8
7.7
8.0
8.1
 1
2
3
4
5.5
9
11
12
15.5
15.5
18
 5.5
7
8
10
13
14
17
19
20
21
A & B
Combined
sum of ranks
96.5
134.5
231
average of ranks
8.8
13.5
11

Our final bit of mechanics is just a dab of symbolic notation.

TA =
the sum of the na ranks in group A
TB =
the sum of the nb ranks in group B
TAB =
the sum of the N ranks in groups A and B combined

For the present example:
TA =
96.5
[with na=11]
TB =
134.5
[with nb=10]
TAB =
231
[with N=21]


¶Logic & Procedure: Method I

The effect of replacing raw measures with ranks is two-fold. The first is that it brings us to focus only on the ordinal relationships among the raw measures—"greater than," "less than," and "equal to"—with no illusion or pretense that these raw measures (4.6, 4.7, 4.9, etc.) derive from an equal-interval scale. The second is that it transforms the data array into a kind of closed system, many of whose properties can then be known by dint of sheer logic.

For example: If you had a total of N=4 items ranked in this fashion, the sum of those ranks would inescapably be

TAB = 1+2+3+4 = 10

This would also be true if some of the ranks were tied; for example:

TAB = 1+2.5+2.5+4 = 10

Similarly for N=5 ranked items:

TAB = 1+2+3+4+5 = 15

And for N=21 ranked items, as in the present example:

TAB = 1+2+3+4+···+18+19+20+21 = 231

In general, the sum of any set of N ranks will be equal to

TAB
=
N(N+1)
2
for N=4:  (4x5)/2=10
for N=5:  (5x6)/2=15
for N=21:  (21x22)/2=231

and the average of the N ranks will of course be that sum divided by N. In any particular case you could calculate the value of TAB in the manner shown above and then divide it by N, though a rather more direct way is to calculate it simply as (N+1)/2, which is what the mean of the N ranks boils down to, once you perform the requisite algebraic juggling:

mean rankAB
=
N(N+1)
2
x
1
N
=
N+1
2
for N=4:  5/2=2.5
for N=5:  6/2=3
for N=21:  22/2=11

Either way, the null hypothesis in our example is that treatments A and B do not differ with respect to their effectiveness. If this were true, then the raw measures within samples A and B would be about the same, on balance, and the rankings that derive from them would be evenly mixed within samples A and B, like cards in a well shuffled deck.

So if the null hypothesis were true, we would expect the separate averages of the A ranks and the B ranks each to approximate this same overall mean value of (N+1)/2=11. This entails that the rank-sums of the two groups, TA and TB, would approximate the values

TA = na(N+1)/2 = 11(21+1)/2 = 121
and
TB = nb(N+1)/2 = 10(21+1)/2 = 110

Thus we know at the outset that
  • the observed value of TA=96.5 belongs to a sampling distribution whose mean is equal to 121T
    andT
  • the observed value of TB=134.5 belongs to a sampling distribution whose mean is equal to 110
Now and again in writings on subjects more or less mathematical, you will find an author saying "It can be shown that such-and-such is so." This typically occurs at junctures where the point to be made is not an obvious one; where it would be a distraction to stop and make it obvious; and where you must therefore ask the reader to take it on faith. This is one of those junctures. For any particular situation of the sort now under consideration, it can be shown that the sampling distributions for TA and TB both have the same variance and the same standard deviation. Here I will show only the structure for the standard deviation, which in the general case is equal to

-T = sqrt
[
nanb(N+1)
12
]

Thus, for the present example, the sampling distributions of TA and TB each have a standard deviation equal to

-T = sqrt
[
(11)(10)(21+1)
12
]
= ±14.2

Another assertion of the "it can be shown" variety is this. In situations where N ranks are distributed within two samples of sizes na and nb, it can be shown that the sampling distributions of TA and TB tend to approximate the form of a normal distribution, providing that na and nb are both equal to or greater than 5. The source of this tendency is similar to what we saw in Chapter 6 when considering the tendency of binomial sampling distributions to approximate the normal.

If the preceding two steps have not been obvious, the next one surely will be. Given the mean and standard deviation of a normally distributed sampling distribution, you can then fold the observed value of either TA or TB into an appropriate version of a z-ratio and refer the result to the unit normal distribution. In this particular context the z-ratio must include a "±.5" correction for continuity, just as with the binomial z-ratio, to accommodate the fact that the sampling distributions of T are intrinsically discrete. (TA and TB can assume decimal values such as 96.5 and 30.5 only as an artifact of the process of assigning tied ranks. Intrinsically, the ranks—1, 2, 3, 4, etc.—on which they are based are all integers.)

Designating

 Tobs  as the observed value of either TA or TB;
-T  as the the mean of the corresponding sampling distribution of T; and
-T  as the standard deviation of that sampling distribution,

the general structure of the ratio is

z
=
(Tobs—T)±.5
T
correction for continuity:
  —.5 when Tobs>T
  +.5 when Tobs<T

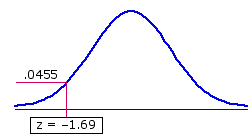
Shown below are the details of calculation for both of our observed T values, TA=96.5 and TB=134.5. Keep in mind that the means of the sampling distributions for TA and TB are 121 and 110, respectively, and that the standard deviation for both distributions is ±14.2.

zA
=
(96.5—121)+.5
14.2
 zB
=
(134.5—110)—.5
14.2
=
—24
14.2
= —1.69
 =
+24
14.2
= +1.69

The remarkable symmetry of zA and zB is no accident. In all instances, zA and zB will have the same absolute value and opposite signs, one positive and the other negative. It therefore makes no difference whether the test of statistical significance is performed with zA or zB. The only requirement is that we keep a clear idea of what a positive or negative sign for z means in any particular case.

In our example, the investigators begin with the directional hypothesis that Treatment A will prove the more effective. This entails that sample A will tend to have the smaller values among the raw measures (indicating lower levels of claustrophobic tendency), hence the smaller ranks, hence an observed value of TA smaller than its null-hypothesis value of 121, hence a value of zA with a negative sign. With the opposite directional hypothesis—that Treatment B will prove the more effective—the expectation would be for zB to end up with the negative sign. With a non-directional hypothesis there would of course be no specific expectation one way or the other.


Critical Values of ±z
Level of Significance for a
Directional Test
.05 .025 .01 .005 .0005
Non-Directional Test
-- .05 .02 .01 .001
zcritical
  1.645     1.960     2.326     2.576     3.291  
Here, at any rate, is the bottom line. If the null hypothesis were true, the mere-chance probability of ending up with a value of zA falling at or beyond (to the left of) z=—1.69 within the normal distribution would be a scant P=.0455. For a directional test, our observed value of zA=—1.69 is therefore significant a bit beyond the basic .05 level. (For a non-directional test it would of course be non-significant, since the mere-chance probability in this case would have to be figured as P=.0455+.0455=.091.)



¶Logic & Procedure: Method II

The limitation of the simple procedure described above is that it is valid only when na and nb are both equal to or greater than 5. This is probably not much of a limitation in actual practice, for one would rarely choose to rely on such tiny samples, except as a last resort. At any rate, if either sample is of a size smaller than 5, it is a different path that must be taken. Up to a point, it is also possible to take this second path even when the sample sizes are both equal to or greater than 5, as in our present example. In this event, the probability assessments arrived at via the two methods are essentially equivalent.

Here as well we begin with some things that can be known by dint of sheer logic. Continuing with our claustrophobia example, recall that TA=96.5 is the sum of the na=11 ranks in sample A and that TB=134.5 is the sum of the nb=10 ranks in sample B.

This first point will be fairly obvious. The maximum possible value of TA in our example would be the sum of the highest na=11 of the ranks:

11+12+13+14+15+16+17+18+19+20+21=176

Similarly, the maximum possible value of TB would be the sum of the highest nb=10 of the ranks:

12+13+14+15+16+17+18+19+20+21=165

For any particular combination of na and nb, these maximum possible values can be reached through the formulas

TA[max]
= nanb +
na(na+1)
2

which for the present example comes out as

TA[max]
= (11)(10) +
11(12)
2
 = 
176

and
TB[max]
= nanb +
nb(nb+1)
2

which comes out as
TB[max]
= (11)(10) +
10(11)
2
 = 
165

Method II of the Mann-Whitney test turns upon the calculation of a measure known as U, which for either sample is equal to the difference between the maximum possible value of T for the sample versus the actually observed value of T. Thus for sample A it would be

UA
= TA[max] — TA
UA
= nanb +
na(na+1)
2
— TA

and for sample B

UB
= TB[max] — TB
UB
= nanb +
nb(nb+1)
2
— TB

For the present example we have already obtained the maximum-possible and observed values for TA and TB:

maximum
possible
value
observed
value
 TA 
176
96.5
 TB 
165
134.5

so we can easily calculate the value of U for this example as either

UA = 176—96.5 = 79.5
or
UB = 165—134.5 = 30.5

It does not matter which of these values you use, so long as you are consistent. The reason it does not matter is that UA and UB are mirror images of each other. For any given values of na and nb, the sum of UA and UB will always be equal to the product of na times nb. Hence the following identities:

UA+UB =
nanb
UA =
nanb—UB
UB =
nanb—UA

The upshot is that once you know one of the values of U, you also implicitly know the other. Note as well that UA and UB are inversely related. The larger the value of one, the smaller must be the value of the other.

We determined earlier that the values of TA and TB that would be expected on the null hypothesis would be TA=121 (versus the observed TA=96.5) and TB=110 (versus the observed TB=134.5). From this you can infer that the values of U to be expected under the null hypothesis are

UA = 176—121 = 55  [vs observed UA = 79.5]
and
UB = 165—110 = 55  [vs observed UB = 30.5]

More generally, the null-hypothesis values of U are given by the identity

UA = UB = (nanb)/2

which for our example would work out as
UA = UB = (11)(10)/2 = 55


On the null hypothesis we would therefore expect the values of UA and UB both to approximate (nanb)/2=55. So if the null hypothesis is true, if there really is no difference in effectiveness between Treatment A and Treatment B, how likely is it that we could end up, by mere chance, with an observed value of UA as large as 79.5; or alternatively, how likely that we could end up with an observed value of UB as small as 30.5?

The principle underlying the answer to this question is but one more verse of a by-now familiar song. First you figure out the total number of possible ways in which N=21 ranks can be combined within two groups of sizes na=11 and nb=10; and then you figure out the proportion of such combinations that would produce a value of UA as large as 79.5, or alternatively a value of UB as small as 30.5.

When I tell you that the total number of possible combinations in this example is

N!
na!nb!
=
21!
11!10!
= 352,716
you will see in a flash that here is yet another instance of "easier said than done." Fortunately, it is also another instance where the bedeviling details have already been worked out. In most hard-copy statistics textbooks you will find a multi-page table of critical values of U, applicable to cases where na and nb are both equal to or less than 20.

I cannot show you the full scope of this table, because it is under copyright and I would have to pay a fee to reproduce it. Fortunately the underlying principles cannot be held in copyright, so what I have done instead is program the following table to calculate some of the critical values of U directly. Enter any particular values of na and nb into the designated cells, click the "Calculate" button, and the corresponding critical values of U will appear in the table. The only restriction is that na and nb must both be between 5 and 20, inclusive. (For cases where the size of either sample is smaller than 5, you will need to consult a table in the back of some hard-copy textbook.) If the two sample-size values are different, you should designate the larger as na and the smaller as nb.

Before you start plugging any new numbers, however, please be sure to read the explanatory text that follows the table.

Critical Values of U for na=, nb=
 Level of Significance for a 
Directional Test
.05
.025
.01
Non-Directional Test
.10
.05
.02
 lower limit 



 upper limit 




As you can see, I have already inserted our current values of na=11 and nb=10, along with the corresponding critical values of U. As illustrated in the next table, each of the pairs of numbers designated "lower limit" and "upper limit" mark the boundaries between which falls a certain proportion of all possible mere-chance combinations of UA and UB in the case where na=11 and nb=10.
lower limit:
upper limit:
  31 
 79 
  26 
 84 
  21 
 89 
.90
 .95
 .98
 proportion between
lower and upper limits
.10
 .05
 .02
proportion outside middle range;
both "tails" combined
.05
 .025
 .01
proportion outside middle range at either end;
each "tail" considered separately.
For the present example our focus can be chiefly on the first pair, 31 and 79. If the null hypothesis is true, there is a 90% chance that UA and UB will both be larger than 31 and both smaller than 79. The remaining possibilities fall outside that range, 5% below it and 5% above. At the one end, there is a 5% chance that UA might end up as large as 79 and UB as small as 31. At the other, there is a 5% chance that UB might end up as large as 79 and UA as small as 31. In our example, the investigators begin with the directional hypothesis that Treatment A will prove the more effective. Specifically, what they expect is
  • that the raw-measure ratings of claustrophobic tendency will be lower in sample A than in sample B; andT
  • that sample A will accordingly tend to have the lower ranks; hence TB>TA and UA>UB
And that is exactly what they do find: UA=79.5, UB=30.5. As these observed values of U fall just outside the range bounded by 31 and 79, we can say that the result is significant just beyond the .05 level for a directional test. For a non-directional test the mere-chance probability of the obtained result would be only a shade below 10%, hence non-significant. (Note that this is the same conclusion we reached earlier with Method I.)

Similarly, the second set of numbers in the table, 26 and 84, mark the boundaries between which fall 95% of all possible mere-chance outcomes. Observed values of U falling at or beyond these boundary points would therefore be significant at or beyond the .05 level for a non-directional test and at or beyond the .025 level for a directional test. And so on for the third set of numbers in the table, marking the lower and upper boundaries for the directional .01 and the non-directional .02 levels of significance.

The VassarStats web site has a page that will perform all steps of the Mann-Whitney test, including the initial rank-ordering of the raw measures.

End of Subchapter 11a.
Return to Top of Subchapter 11a
Go to Chapter 12 [t-Test for Two Correlated Samples]


Home Click this link only if the present page does not appear in a frameset headed by the logo Concepts and Applications of Inferential Statistics