©Richard Lowry, 1999-
All rights reserved.
Chapter 17.
One-Way Analysis of Covariance for Independent Samples
Part 2
¶Example 1. Comparative Effects of Two Methods of Hypnotic Induction
| X = the score on the index of primary suggestibility Y = the score on the index of hypnotic induction |
| Method A | Method B| Sub- | ject Xa | Ya | Sub- | ject Xb | Yb |
a1 | a2 a3 a4 a5 a6 a7 a8 a9 a10
5 | 10 12 9 23 21 14 18 6 13
20 | 23 30 25 34 40 27 38 24 31
b1 | b2 b3 b4 b5 b6 b7 b8 b9 b10
7 | 12 27 24 18 22 26 21 14 9
19 | 26 33 35 30 31 34 28 23 22 Means | 13.1 | 29.2 |
| 18.0 | 28.1 | | |||||
| If you have not already done so, please click here to place a version of the data table into the frame on the left. |
A basic one-way analysis of covariance requires four sets of calculations. In the first set you will clearly recognize the analysis-of-variance aspect of ANCOVA. The two middle sets are aimed at the covariance aspect, and the final set ties the two aspects together. As in earlier chapters, SS refers to the sum of squared deviates. The designation SC in the third set refers to the sum of co-deviates, the raw measure of covariance introduced in Chapter 3. In both cases, the subscripts "T," "wg," and "bg" refer to "Total," "within-groups," and "between-groups," respectively.
- SS values for Y, the dependent variable in which one is chiefly interested.T
Items to be calculated:
SST(Y)
SSwg(Y)
SSbg(Y)
- SS values for X, the covariate whose effects upon Y one wishes to bring under statistical control.
Items to be calculated:
SST(X)
SSwg(X)
- SC measures for the covariance of X and Y;
Items to be calculated:
SCT
SCwg
- And then a final set of calculations, which begin by removing from the Y variable the portion of its variability that is attributable to its covariance with X.
1. Calculations for the Dependent Variable Y
The following table shows the values of Y along with the several summary statistics required for the calculation of SST(Y), SSwg(Y), and SSbg(Y):
| Ya | Yb|
|
20 | 23 30 25 34 40 27 38 24 31
19 | 26 33 35 30 31 34 28 23 22 for total array of data
|
| Click here if you wish to see the details of calculation for this data set. N | 10 | 10 | 20 |
| SST(Y) = 668.5 SSwg(Y) = 662.5 SSbg(Y) = 6.0 .∑Yi
| 292 | 281 | 573 | .∑Yi2
| 8920 | 8165 | 17085 | SS | 393.6 | 268.9 |
| Mean | 29.2 | 28.1 | 28.7 | |
|
Just as an aside, note the discrepancy between SSbg(Y)=6.0 [0.9% of total variability] and SSwg(Y)=662.5 [99.1% of total variability] This reflects the fact mentioned earlier, that the mean difference between the groups is quite small in comparison with the variability that exists inside the groups. |
2. Calculations for the Covariate X
The next table has the same structure as the one above, but now what we show are the values of X along with the several summary statistics required for the calculation of SST(X) and SSwg(X). (We need not bother with SSbg(X), since it does not enter into any subsequent calculations.)
| Xa | Xb|
|
5 | 10 12 9 23 21 14 18 6 13
7 | 12 27 24 18 22 26 21 14 9 for total array of data
|
| Click here if you wish to see the details of calculation for this data set. N | 10 | 10 | 20 |
| SST(X) = 908.9 SSwg(X) = 788.9 .∑Xi
| 131 | 180 | 311 | .∑Xi2
| 2045 | 3700 | 5745 | SS | 328.9 | 460.0 |
| Mean | 13.1 | 18.0 | 15.6 | |
3. Calculations for the Covariance of X and Y
You will recall from Chapter 3 that the raw measure of the covariance between two variables, X and Y, is a quantity known as the sum of co-deviates:
SC = ∑(Xi—MX)(Yi—MY) | (Xi—MX) = deviateX (Yi—MY) = deviateY (Xi—MX)(Yi—MY) = co-deviateXY |
which for practical computational purposes can be expressed as
| SC | = ∑(XiYi) — | (∑Xi)(∑Yi) N |
We will be calculating two separate values of SC: one for the covariance of X and Y within the total array of data, and another for the covariance within the two groups.
The next table shows the cross-products of Xi and Yi for each subject in each of the two groups. (E.g., the first subject in group A had
Groups| A | B |
| For group A: o∑Xai = 131 o∑Yai = 292 For group B: o∑Xbi = 180 o∑Ybi = 281 For total array: o∑XTi = 311 o∑YTi = 573 XaYa | XbYb |
100 | 230 360 225 782 840 378 684 144 403
133 | 312 891 840 540 682 884 588 322 198 for total array of data Sums | 4146 | 5390 | 9536 |
| .∑(XaiYai) | .∑(XbiYbi) | .∑(XTiYTi) | | ||||
On the basis of the summary values presented in this table you can then easily calculate SC for the total array of data as
| SCT | = ∑(XTiYTi) — | (∑XTi)(∑YTi) NT |
| SCT | = 9536 — | (311)(573) 20 | = 625.9 |
The values of SC within each of the two groups can be calculated similarly as
For Group A:
|
| SCwg(a)
| = ∑(XaiYai) —
| (∑Xai)(∑Yai) | Na | |||
| SCwg(a) | = 4146 — | (131)(292) 10 | = 320.8 |
For Group B:
|
| SCwg(b)
| = ∑(XbiYbi) —
| (∑Xbi)(∑Ybi) | Nb | |||
| SCwg(b) | = 5390 — | (180)(281) 10 | = 332.0 |
the sum of which will then yield the within-groups covariance measure of
| SCwg | = SCwg(a) + SCwg(b)|
|
|
| = 320.8 + 332.0 = 652.8 | |
4. The Final Set of Calculations
We begin with a summary of the values of SS and SC obtained so far, as these will be needed in the calculations that follow. Recall that Y is the variable in which we are chiefly interested, and X is the covariate whose effects we are seeking to remove.
| X | Y | Covariance|
|
SST(X) = 908.9 | SSwg(X) = 788.9
|
SST(Y) = 668.5 | SSwg(Y) = 662.5 SSbg(Y) = 6.0
|
SCT = 625.9 | SCwg = 652.8
|
For handy reference, click here to place a version of | this table into the frame on the left.] | |||||||
4a. Adjustment of SST(Y)
From Chapter 3 you know that the overall correlation between X and Y (both groups combined) can be calculated as
| rT | = |
SCT sqrt[SST(X) x SST(Y)] | 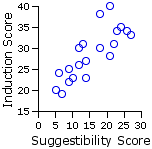
| |||||
| = |
625.9 sqrt[908.9 x 668.5]
|
| = | +.803 | |
The proportion of the total variability of Y attributable to its covariance with X is accordingly
|
(rT)2 = (+.803)2 = .645 |
In the first step of this series, we adjust SST(Y) by removing from it this proportion of covariance. Given
|
668.5 x .645 = 431.2 |
|
668.5—431.2 = 237.3 [tentative] |
I have marked the above result as tentative because a calculation based on r2 is likely to produce rounding errors [in the present example, the 0.645 value used for (rT)2 is rounded from 0.64475...]. For practical purposes, one is better advised to use the following algebraically equivalent computational formula:
|
[adj]SST(Y) | = SST(Y)— |
(SCT)2 SST(X) | "[adj]" = "adjusted"
|
| = 668.5 — | (625.9)2 | 908.9
|
| = 237.5 | | |||
4b. Adjustment of SSwg(Y)
By analogy, the aggregate correlation between X and Y within the two groups can be calculated as
| rwg | = |
SCwg sqrt[SSwg(X) x SSwg(Y)] | 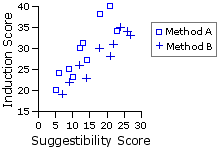
| ||||
| = |
652.8 sqrt[788.9 x 662.5]
| = | +.903 | |
The proportion of the within-groups variability of Y attributable to covariance with X is therefore
|
(rwg)2 = (+.903)2 = .815 |
The amount of SSwg(Y)(=662.5) to be removed is accordingly
|
662.5 x .815 = 539.9 |
|
662.5—539.9 = 122.6 [tentative] |
Here again the result is marked tentative on account of the possibility of rounding errors. The more precise result is given by the following computational formula:
|
[adj]SSwg(Y) | = SSwg(Y)— |
(SCwg)2 SSwg(X)
|
| = 662.5 — | (652.8)2 | 788.9
|
| = 122.3 | | ||
4c. Adjustment of SSbg(Y)
The adjusted value of SSbg(Y) can then be obtained through simple subtraction as
|
[adj]SSbg(Y) | = |
[adj]SST(Y)
— [adj]SSwg(Y)|
|
| = | 237.5 — 122.3 = 115.2 | |
4d. Adjustment of the Means of Y for Groups A and B

| bwg | = | SCwg SSwg(X)
|
|
| = | 652.8 | 788.9 = +.83 |
| |
| MX | MY| group A | 13.1 | 29.2 | group B | 18.0 | 28.1 | combined | 15.55 | 28.65 | |
[adj]MYa = 29.2 + (2.45x.83) = 31.23
| and
|
| [adj]MYb = 28.1 — (2.45x.83) = 26.07
| | ||
This is the conceptual structure for the adjustment of the means of Y for the groups. Once you have the concept, the mechanics of the process can be accomplished somewhat more expeditiously via the following computational formula:
For Group A:|
|
| [adj]MYa | = MYa — bwg(MXa—MXT) |
|
|
| = 29.2 — .83(13.1—15.55) |
|
|
| = 31.23 | | |||
For Group B:|
|
| [adj]MYb | = MYb — bwg(MXb—MXT) |
|
|
| = 28.1 — .83(18.0—15.55) |
|
|
| = 26.07 | | |||
4e. Analysis of Covariance Using Adjusted Values of SS
As with the corresponding one-way ANOVA, the final step in a one-way analysis of covariance involves the calculation of an
| F = | MSeffect MSerror | = | MSbg MSwg | = | SSbg/dfbg SSwg/dfwg |
The only difference is that now we are using the adjusted values of SSbg(Y) and SSwg(Y), along with one adjusted value of df. In the basic analysis of variance, the degrees of freedom for the within-groups variance is
| [adj]dfwg(Y) = NT—k—1 | for the present example: 20—2—1 = 17 |
| dfbg(Y) = k—1 | for the present example: 2—1 = 1 |
Given [adj]SSbg(Y)=115.2 and [adj]SSwg(Y)=122.3, our F-ratio for the analysis of covariance is accordingly
| F | = | [adj]SSbg(Y)/dfbg(Y) [adj]SSwg(Y)/[adj]dfwg(Y)
|
|
| = | 115.2/1 | 122.3/17
|
|
|
| = | 16.01 [with df=1,17] | | |||
| df denomi- nator | df numerator| 1 | 2 | 3 | 17 | 4.45 | 8.40 3.59 | 6.11 3.20 | 5.19 | ||
MYa=29.2 versus MYb=28.1
|
| |
-
If the correlation between X and Y within the general population is approximately the same as we have observed within the samples; andT
If we remove from Y the covariance that it has with X, so as to remove from the analysis the pre-existing individual differences that are measured by the covariate X; andT
If we adjust the group means of Y in accordance with the observed correlation between X and Y;T
Then we can conclude that the two adjusted means
| [adj]MYa=31.23 versus [adj]MYb=26.07 |
¶Assumptions of ANCOVA
The analysis of covariance has the same underlying assumptions as its parent, the analysis of variance. It also has the same robustness with respect to the non-satisfaction of these assumptions, providing that all groups have the same number of subjects. There is, however, one assumption that the analysis of covariance has in addition, by virtue of its co-descent from correlation and regression—namely, that the slopes of the regression lines for each of the groups considered separately are all approximately the same.
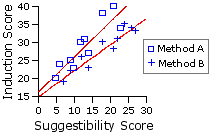
End of Chapter 17, Part 2.
Return to Top of Chapter 17, Part 2
Go to Chapter 17, Part 3
| Home | Click this link only if the present page does not appear in a frameset headed by the logo Concepts and Applications of Inferential Statistics |