©Richard Lowry, 1999-
All rights reserved.
Chapter 17.
One-Way Analysis of Covariance for Independent Samples
Part 3
¶Example 2. Three Methods of Instruction for Elementary Computer Programming
| Method A | Method B | Method C | 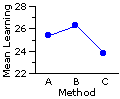
| |||
|
29 24 14 27 27 28 27 32 13 35 32 17 |
15 28 13 36 29 27 31 33 32 15 30 26 |
32 27 15 23 26 17 25 14 29 22 30 25 means |
25.4 |
26.3 |
23.8 | |
Given the differences among the means of the three groups, you might think at first glance that Method B has the edge over Method A, and that Methods B and A are both superior to Method C. As it happens, however, these differences, considered in and of themselves, are well within the range of mere random variability. A simple one-way ANOVA performed on this set of data would yield a miniscule
The reason for this shortfall is of course the degree of variability within the groups, which is quite large in comparison with the mean differences that appear between the groups. Well aware of the broad range of pre-existing individual differences that are likely to be found in situations of this sort, our curriculum researcher took the precaution of measuring her subjects beforehand with respect to their pre-existing levels of basic computer familiarity. The rationale is fairly obvious: the more familiar a subject is with basic computer procedures, the more of a head start he or she will have in learning the elements of computer programming; remove the effects of this covariate, and you thereby remove a substantial portion of the extraneous individual differences. Our researcher was also well aware that her three groups, drawn from three different schools, might be starting out with substantially different levels of basic computer familiarity, in consequence of the average socio-economic differences that she knows to exist among the schools. The groups instructed by Methods A and B both reside in fairly affluent neighborhoods, while the group instructed by Method C comes from a less privileged part of town.
The following table shows the measures on both variables laid out in a form suitable for an analysis of covariance, with
| X = | the prior measure of basic computer familiarity [The covariate whose effects the investigator wishes to remove from the analysis.] and |
| Y = | the measure of how well the subject has learned | the elementary programming material [The dependent variable in which the investigator is chiefly interested.] | ||
| Method A | Method B | Method C| Sub- | ject Xa | Ya | Sub- | ject Xb | Yb | Sub- | ject Xc | Yc |
a1 | a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12
14 | 10 7 18 14 16 13 15 5 18 16 10
29 | 24 14 27 27 28 27 32 13 35 32 17
b1 | b2 b3 b4 b5 b6 b7 b8 b9 b10 b11 b12
6 | 16 9 19 13 14 15 18 17 8 15 16
15 | 28 13 36 29 27 31 33 32 15 30 26
c1 | c2 c3 c4 c5 c6 c7 c8 c9 c10 c11 c12
15 | 9 7 12 12 9 12 3 13 10 11 8
32 | 27 15 23 26 17 25 14 29 22 30 25 Means | 13.0 | 25.4 |
| 13.8 | 26.3 |
| 10.1 | 23.8 | | ||||||||||
As you can see from the means in the X columns, the investigator was right in her expectations concerning different group levels of basic computer familiarity: 13.0 and 13.8 for groups A and B, versus 10.1 for group C. So once again we encounter the
The computational format for the one-way ANCOVA is the same here as for Example 1. The only structural difference is that now the number of groups
1. Calculations for the Dependent Variable Y
Values of Y along with the several summary statistics required for the calculation of SST(Y), SSwg(Y), and SSbg(Y):
| Ya | Yb | Yc|
|
29 | 24 14 27 27 28 27 32 13 35 32 17
15 | 28 13 36 29 27 31 33 32 15 30 26
32 | 27 15 23 26 17 25 14 29 22 30 25 for total array of data N | 12 | 12 | 12 | 36 |
| . | 305 | 315 | 285 | 905 | . | 8315 | 8919 | 7143 | 24377 | SS | 562.9 | 650.3 | 374.3 |
| Mean | 25.4 | 26.3 | 23.8 | 25.1 | |
2. Calculations for the Covariate X
Values of X along with the several summary statistics required for the calculation of SST(X) and SSwg(X).
| Xa | Xb | Xc|
|
14 | 10 7 18 14 16 13 15 5 18 16 10
6 | 16 9 19 13 14 15 18 17 8 15 16
15 | 9 7 12 12 9 12 3 13 10 11 8 for total array of data N | 12 | 12 | 12 | 36 |
| SST(X) = 581.6 SSwg(X) = 488.6 . | 156 | 166 | 121 | 443 | . | 2220 | 2482 | 1331 | 6033 | SS | 192.0 | 185.7 | 110.9 |
| Mean | 13.0 | 13.8 | 10.1 | 12.3 | |
3. Calculations for the Covariance of X and Y
Cross-products of Xi and Yi for each subject in each of the three groups, along with other summary data required for the calculation of SCT and SCwg:
| A | B | C | ||||||||||||
| XaYa | XbYb | XcYc|
(14)(29) = 406 | (10)(24) = 240 (7)(14) =98 (18)(27) = 486 (14)(27) = 378 (16)(28) = 448 (13)(27) = 351 (15)(32) = 480 (5)(13) =65 (18)(35) = 630 (16)(32) = 512 (10)(17) = 170
(6)(15) =90 | (16)(28) = 448 (9)(13) = 117 (19)(36) = 684 (13)(29) = 377 (14)(27) = 378 (15)(31) = 465 (18)(33) = 594 (17)(32) = 544 (8)(15) = 120 (15)(30) = 450 (16)(26) = 416
(15)(32) = 480 | (9)(27) = 243 (7)(15) = 105 (12)(23) = 276 (12)(26) = 312 (9)(17) = 153 (12)(25) = 300 (3)(14) =42 (13)(29) = 377 (10)(22) = 220 (11)(30) = 330 (8)(25) = 200 for total array of data .∑(XaiYai) | =4264 .∑(XbiYbi) | =4683 .∑(XciYci) | =3038 .∑(XTiYTi) | =11985 o∑Xai=156 | o∑Yai=305 o∑Xbi=166 | o∑Ybi=315 o∑Xci=121 | o∑Yci=285 o∑XTi=443 | o∑YTi=905 |
Calculation of SC for the total array of data:
| SCT | = ∑(XTiYTi) — | (∑XTi)(∑YTi) NT |
| SCT | = 11985 — | (443)(905) 36 | = 848.5 |
Calculation of SCwg:
The components for each group ("g") are calculated as:
| SCwg(g) | = ∑(XgiYgi) — | (∑Xgi)(∑Ygi) Ng |
Thus:
| SCwg(a) | = 4264 — | (156)(305) 12 | = 299.0 |
| SCwg(b) | = 4683 — | (166)(315) 12 | = 325.5 |
| SCwg(c) | = 3036 — | (121)(285) 12 | = 164.3 |
| SCwg | = SCwg(a) + SCwg(b) + SCwg(c)|
|
|
| = 299.0 + 325.5 + 164.3 = 788.8 | |
4. The Final Set of Calculations
Here again is a summary of the values of SS and SC obtained so far. Recall that Y is the variable in which we are chiefly interested, and X is the covariate whose effects we are seeking to remove.
| X | Y | Covariance|
|
SST(X) = 581.6 | SSwg(X) = 488.6
|
SST(Y) = 1626.3 | SSwg(Y) = 1587.4 SSbg(Y) = 38.9
|
SCT = 848.5 | SCwg = 788.8
|
For handy reference, click here to place a version of | this table into the frame on the left.] | |||||||
4a. Adjustment of SST(Y)
As indicated in connection with Example 1, the overall correlation between X and Y (all three groups combined) can be calculated as
| rT | = |
SCT sqrt[SST(X) x SST(Y)] | 
| |||||
| = |
848.5 sqrt[581.6 x 1626.31]
|
| = | +.872 | |
The proportion of the total variability of Y attributable to its covariance with X is accordingly
|
(rT)2 = (+.872)2 = .760 |
As previously noted, the removal of this portion is best accomplished (minimizing the risk of rounding errors) through the computational formula
|
[adj]SST(Y) | = SST(Y)— |
(SCT)2 SST(X)
|
| = 1626.3 — | (848.5)2 | 581.6
|
| = 388.4 | | ||
4b. Adjustment of SSwg(Y)
Similarly, the aggregate correlation between X and Y within the three groups can be calculated as
| rwg | = |
SCwg sqrt[SSwg(X) x SSwg(Y)] | 
| |||||
| = |
788.8 sqrt[488.6 x 1587.4]
|
| = | +.896 | |
So the proportion of the within-groups variability of Y attributable to covariance
|
(rwg)2 = (+.896)2 = .803 |
Here again, the removal of this portion is best accomplished through the computational formula
|
[adj]SSwg(Y) | = SSwg(Y)— |
(SCwg)2 SSwg(X)
|
| = 1587.4 — | (788.8)2 | 488.6
|
| = 314.0 | | ||
4c. Adjustment of SSbg(Y)
The adjusted value of SSbg(Y) can then again be obtained through simple subtraction as
|
[adj]SSbg(Y) | = |
[adj]SST(Y)
— [adj]SSwg(Y)|
|
| = | 388.4 — 314.0 = 74.4 | |
4d. Adjustment of the Means of Y for Groups A, B, and B
The average relationship between
| bwg | = | SCwg SSwg(X) | 
| ||||
| = | 788.8 488.6 | = +1.61|
| | ||||
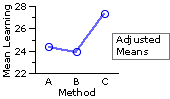
| MX | observed MY | adjusted MY group A | 13.0 | 25.4 | 24.3 | group B | 13.8 | 26.3 | 23.9 | group C | 10.1 | 23.8 | 27.3 | combined | 12.3 | 25.1 | |
| [adj]MYa | = MYa — bwg(MXa—MXT)|
|
|
| = 25.4 — 1.61(13.0—12.3) |
|
|
| = 24.3 | | |
| [adj]MYb | = MYb — bwg(MXb—MXT)|
|
|
| = 26.3 — 1.61(13.8—12.3) |
|
|
| = 23.9 | | |
| [adj]MYc | = MYc — bwg(MXc—MXT)|
|
|
| = 23.8 — 1.61(10.1—12.3) |
|
|
| = 27.3 |
| | ||||
| As illustrated in the adjacent graph, the adjusted group means paint quite a different picture. When the different pre-existing levels of basic computer familiarity are taken into account, Method C appears to have a substantial edge over both of the other instructional methods. | 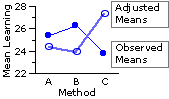
|
4e. Analysis of Covariance Using Adjusted Values of SS
The simple computational format for this step is the same as for Example 1. All we need do here is lay out its results in the form of an ANCOVA summary table:
| Source | SS | df | MS | F | P| adjusted means | [between-groups effect] 74.4 | 2 | 37.2 | 3.8 | <.05 | adjusted error | [within-groups] 314.0 | 32 | 9.8 | adjusted total | 388.4 | 34 | |
| [Recall that dfbg(Y)=k—1 and [adj]dfwg(Y)=NT—k—1] |
| df denomi- nator | df numerator| 1 | 2 | 3 | 32 | 4.15 | 7.50 3.29 | 5.34 2.90 | 4.46 | ||
- If the correlation between
X and Y within the general population is approximately the same as we have observed within the samples; andT
- If we remove from Y the covariance that it has with X, so as to remove from the analysis the pre-existing individual differences that are measured by the covariate X; andT
- If we adjust the group means of Y in accordance with the observed correlation between
X and Y;T
- Then we can conclude that the three adjusted means significantly differ in the degree indicated,
namely, P<.05. - If we adjust the group means of Y in accordance with the observed correlation between
|
¶Test for Homogeneity of Regression
As mentioned toward the end of Part 2, the analysis of covariance assumes that the slopes of the regression lines for each of the groups considered separately do not significantly differ from the slope of the overall within-groups regression, which for the present example
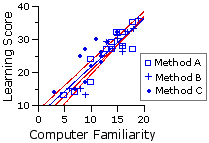
The procedure for rigorously determining whether this "homogeneity of regression" assumption is satisfied involves yet another variation on the theme of analysis of variance. As in all versions of ANOVA, the end result is an
| F = | MSeffect MSerror | = | SSeffect /dfeffect SSerror /dferror |
In the present version, the sum of squared deviates
- For each group ("g"), calculate
(SCg)2
SSXg
Note thatSCg/SSXg
would give you the slope for group g.
- Sum up the results of step 1 and subtract from that sum the quantity
(SCwg)2
SSwg(X)
Note thatSCwg/SSwg(X) = bwg
the slope for the overall within-groups regression.
Hence:
SSb-reg = 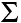
(SCg)2
SSXg
—
(SCwg)2
SSwg(X)
which for the present example, using previously calculated values, comes out toSSb-reg
=
(SCa)2
SSXa
+
(SCb)2
SSXb
+
(SCc)2
SSXc
—
(SCwg)2
SSwg(X)
SSb-reg
=
(299.0)2
192.0
+
(325.5)2
185.7
+
(164.3)2
110.9
—
(788.8)2
488.6
SSb-reg
=
6.1
The sum of squared deviates
| SSY(remainder) | = [adj]SSwg(Y) — SSb-reg|
|
| = 314.0 — 6.1 = 307.9 |
|
| = 307.9 | |
The apportionment of degrees of freedom follows the same pattern. The value of [adj]SSwg(Y) that appears in the original ANCOVA starts out with degrees of freedom equal to
| [adj]dfwg(Y) | = NT — k — 1|
|
| = 36 — 3 — 1 |
|
| = 32 | |
When you remove SSb-reg from [adj]SSwg(Y), you are also removing the number of degrees of freedom that go along with it, which is
| dfb-reg | = k — 1|
|
| = 3 — 1 |
|
| = 2 | |
So the degrees of freedom for SSY(remainder) is
| dfY(remainder) | = [adj]dfwg(Y) — dfb-reg|
|
| = (NT—k —1)—(k —1) |
|
| = 32 — 2 = 30 | |
calculate [adj]dfwg(Y) as NT—2k.
With these components at hand we can then calculate the
| F | = | MSb-reg MSY(remainder) | = | SSb-reg /dfb-reg SSY(remainder) /dfY(remainder)
|
|
| = | 6.1/2 | 307.9/30
|
|
| = | 0.30 | [with df = 2,30] | | ||
| df denomi- nator | df numerator| 1 | 2 | 3 | 30 | 4.17 | 7.56 3.32 | 5.39 2.92 | 4.51 | ||
In Chapter 18 we will extend the analysis of covariance to the case where there are two independent variables, on analogy with the two-way analysis of variance for independent samples examined in Chapter 16.
End of Chapter 17, Part 3.
Return to Top of Chapter 17, Part 3
Go to Chapter 18 [This link is not yet active.]
| Home | Click this link only if the present page does not appear in a frameset headed by the logo Concepts and Applications of Inferential Statistics |