The analysis of covariance, often referred to by its acronym ANCOVA, is the result of a felicitous marriage between

1. the analysis of variance, as examined in Chapters 13 through 16, and
2. the concepts and procedures of linear correlation and regression, as examined in Chapter 3.

It is, in fact, a veritable powerhouse of a statistical procedure, and I am surprised it is not used more often. Like the correlated-samples designs for t-tests (Chapter 12) and the analysis of variance (Chapter 15), it is capable of removing the obscuring effects of pre-existing individual differences among subjects. It does this, however, without resorting to the repeated-measures strategy of testing each subject under each of the several experimental conditions. In consequence, it is able to avoid the potential complications of having subjects tested first in one condition, then in another, and then perhaps in yet another.

---

In the correlated-samples design, it is typically assumed that these potential sequencing effects can be obviated by systematic counter-balancing. With two experimental conditions, A and B, you would test half your subjects in the sequence A·B and the other half in the sequence B·A. With three conditions, you would test equal numbers of your subjects in the six possible sequences: A·B·C, A·C·B, B·A·C, B·C·A, C·A·B, C·B·A. And so on.

But there are certain kinds of situations where a repeated-measures design might not be feasible; and there are others where, even if it is feasible, it might not be desirable. If you were interested in determining which of two methods of elementary mathematics instruction is more effective, it would clearly make no sense to have half your subjects taught first by Method A, then by Method B, and the other half taught first by Method B, then by Method A. Analogously, suppose you were interested in determining which of two methods of hypnotic induction is the more effective. Here it would certainly be possible to test each of your subjects under each of the two conditions—half in the sequence A·B and the other half in the sequence B·A—though I suspect you would end up with a substantial sequencing effect, even with the counter-balancing. By the time the A·B subjects get to Method B, they will have already experienced Method A; and that prior experience is likely to influence their response to Method B. Similarly for the B·A subjects: their responses to Method A are likely to be substantially influenced by their prior experience with Method B. In these two cases and in many others, the analysis of covariance provides the best of both worlds: for it allows you to examine the several experimental conditions independently, in isolation from each other, while at the same time removing from the situation the obscuring effects of pre-existing individual differences.

---

This, however, is only the first part of its strength. An even greater advantage of the analysis of covariance is that it allows you to compensate for systematic biases among your samples. To return for the moment to the example of two methods of elementary mathematics instruction, suppose you were to begin with a subject pool of 20 third-graders, randomly sorting them into two independent groups of 10 subjects each, with the design of teaching one group by Method A and the other by Method B. The aim of the initial random sorting is to ensure that the two groups are starting out approximately equal, on average, with respect to all factors that might be pertinent to how well they are likely to respond to elementary mathematics instruction. Nonetheless it could happen through sampling error—another name for sheer, cussed random variability—that the two groups do not start out on an equal footing with respect to one or another of these factors. To take the obvious examples, it could happen through mere chance coincidence in the sorting process that one of the groups starts out with a higher average level of intelligence or motivation, either one of which would surely complicate the situation. The analysis of covariance provides a way of measuring and removing the effects of such initial systematic differences between the samples.

---

The procedures of ANCOVA achieve these useful results through an application of the concept of covariation, which you will recall from Chapter 3 is what underlies the whole apparatus of linear correlation and regression. In any particular research situation, the individual differences that appear within your measures on the variable of interest are potentially correlated with something else. If the variable of interest is a measure of how well subjects learn elementary mathematics under one or the other of two methods of instruction, the potential correlates are likely to include such items as prior relevant learning, motivation, attention, self-discipline, and sheer intelligence. We will focus for the moment on intelligence, which is surely not the least of these correlates. Suppose we had a prior measure of intelligence for each subject in each of two randomly sorted independent groups. One group receives instruction by Method A, the other by Method B; and we then follow up by measuring each subject with respect to how well he or she has learned the designated subject matter. The result is two sets of bivariate measures, one set for each group. In keeping with the language of correlation and regression, we will designate these measures as X and Y. Thus

	X =	the measure of intelligence
	Y =	the measure of learning

Suppose, now, that we were actually to perform this experiment and end up with the results listed in the following table. For the sake of simplicity, I am showing only 4 subjects per group; in real-life research you would rarely want to have such tiny samples. I am also color-coding the values of X and Y to help you keep this cast of characters straight.

	Method A				Method B
Subject	Xa	Ya		Subject	Xb	Yb
a1   a2   a3   a4	88   98 100 110	66 85 90 97		b1   b2   b3   b4	90 100 110 120	62 87 91 98
Means	99.0	84.5			105.0	84.5

I have designed this set of data to make two things obvious at a glance: First, that there is a considerable range of individual differences within the values of X and Y for each of the two groups; and second, that the values of X and Y within each group have a high positive correlation. In brief, and not surprisingly: the higher the measure of intelligence (X), the higher the measure of learning (Y). Not to put too fine a point on it: the smarter a subject is at the outset, the more likely it is that he or she will learn more rather than less, irrespective of the method of instruction. So a substantial portion of the variability that occurs within each of the sets of Y measures is actually covariance with the corresponding set of X measures. Remove that covariance from Y and you thereby remove a substantial portion of the extraneous variability of individual differences.

The second thing I have designed into this set of data is an outcome in which the means of the two sets of Y measures (learning) are precisely the same: M_Ya=M_Yb=84.5. While this precise identity of two group means would not often occur in real-life settings, it is a useful contrivance to make a point. If you were to look at M_Ya and M_Yb in isolation from the rest of the data, they would seem to be suggesting that Method A and Method B do not differ. Examine them, however, in conjunction with the information provided by the X measures (intelligence), and you will see another possibility.

	Method A			Method B
	Xa	Ya		Xb	Yb
Means	99.0	84.5		105.0	84.5

By mere chance coincidence, the initial random sorting gave us two groups with different mean levels of intelligence: M_Xa=99.0 versus M_Xb=105.0. If there truly were no difference between Method A and Method B, we could reasonably expect that the higher mean intelligence of group B would have produced a higher mean level of learning. As it did not produce a higher mean level of learning, we can reasonably entertain the possibility that Method A would have proved the more effective, if only the two groups of subjects had started out on an equal footing. The analysis of covariance permits you to examine a possibility of this sort by way of a kind of what-if scenario. For this particular example: What would have happened if the two groups had started out with equivalent mean levels of intelligence? Or more generally: What would have happened if the several (two or more) groups had started out with equivalent mean levels of the covariate (intelligence, prior learning, motivation, or whatever else the relevant covariate might be).

---

We will work through two computational examples of a one-way ANCOVA, the first for k=2 and the second for k=3. (As in a one-way ANOVA, k refers to the number of levels of the independent variable.) In introducing Example 1, I will be taking a bit more time to sketch the Big Picture of ANCOVA because its computational side is rather complex and, once we get into it, there will be a certain risk of becoming lost in the details.

---

¶Example 1. Comparative Effects of Two Methods of Hypnotic Induction

This example is a follow-up on an item briefly mentioned above, structurally similar to the elementary-mathematics illustration, though with a somewhat more exotic setting. A team of researchers is interested in determining whether two methods of hypnotic induction, A and B, differ with respect to their effectiveness. They begin by randomly sorting 20 volunteer subjects into two independent groups of 10 subjects each, with the aim of administering Method A to one group and Method B to the other. But then, before either of the induction methods is administered, each subject is pre-measured on a standard index of "primary suggestibility," which is a variable known to be correlated with receptivity to hypnotic induction. The dependent variable, measured during the administration of Method A or Method B, is the subject's score on a standard index of hypnotic induction. Thus

	X =	the score on the index of primary suggestibility
	Y =	the score on the index of hypnotic induction

The following table shows the scores on both variables for each subject in each of the two groups. Also shown are the means of the four sets of measures.

	Method A				Method B
Sub- ject	Xa	Ya		Sub- ject	Xb	Yb
a1   a2   a3   a4   a5   a6   a7   a8   a9   a10	5 10 12   9 23 21 14 18   6 13	20 23 30 25 34 40 27 38 24 31		b1   b2   b3   b4   b5   b6   b7   b8   b9   b10	7 12 27 24 18 22 26 21 14   9	19 26 33 35 30 31 34 28 23 22
Means	13.1	29.2			18.0	28.1
X = suggestibility scoreT Y = induction score

---

As promised, here is a bit more on the Big Picture before we get into the computational details. In particular, I want to try to convey a sense of why one might bother with the analysis of covariance in a situation of this sort, rather than just performing a simple t-test or analysis of variance. First, please click here to place a version of the data table for Example 1 into the frame on the left. This will allow you to look back and forth at the data without having to scroll up and down within the present frame. (Later you can click one of the lines labeled "Return to Contents" to restore the left frame to its original setting.)

I'll ask you to begin by focusing on the two sets of induction scores, Y, the variable in which we are chiefly interested. We noted in Chapter 14 that with two independent samples the procedures for ANOVA and t are logically equivalent, with F = t². If you were to plug these values of Y into either a t-test or an analysis of variance, the result in each case would fall far short of significance at the basic .05 level: t=+.40 [df=18]; F=.16 [df=1,18]. These non-significant values of t and F reflect the fact, illustrated in Figure 17.1, that the mean difference between the two groups of induction scores (29.2—28.1=1.1) is quite small in comparison with the large amount of variability that occurs within the groups.

Figure 17.1. Variability of Induction Scores within Groups A and B_T

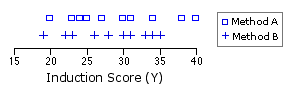
MYa = 29.2 MYb = 28.1

The bottom line here is that the induction scores, considered in and of themselves, would suggest that there is no particular difference between Method A and Method B, one way or the other.

But now see what happens when we look concurrently at the covariate X, "primary suggestibility." As shown in Figure 17.2, a substantial portion of the variability among the induction scores (both groups combined) is associated with pre-existing individual differences in suggestibility. In brief: the greater the level of pre-existing receptivity to hypnotic induction, the greater the response to the induction method.

Figure 17.2. Correlation between X and Y: Both Groups Combined_T

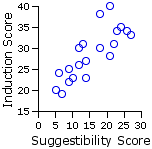
r = +.803T   r2 = .645

The upshot of the correlation between X and Y is simply this:

Given r2 = .645:T Of all theTvariability that exists among the induction scores (Y), 65.4% can be traced to pre-existing individual differences in primary suggestibility (X).

As you will see a bit later, this is the precise amount by which the analysis of covariance will be reducing the total variability of the induction scores (both groups combined). Following the same logic, though with different numbers, there will also be a reduction of within-groups variability and a corresponding increase in the relative weight of the mean difference between the two groups. Overall, the analysis of covariance removes from Y the portion of its variability that is attributable to covariation with X, and focuses only on what is left over (the "residual variance") following this removal. [If your memory of these matters has grown a bit dim since Chapter 3, please click here for a brief refresher course.]

And then there is also this to fold into the mix. The aim of the initial random sorting was to ensure that the two groups were starting out approximately equal, on average, with respect to all factors that might be relevant to how well they were likely to respond to any particular method of hypnotic induction. But random variability being the tricky thing that it is, they in fact end up with substantially different mean levels of the key covariate "primary suggestibility." The following abbreviated version of the data table will give you an overview of this portion of the picture.

	Method A			Method B
	Xa	Ya		Xb	Yb
Means	13.1	29.2		18.0	28.1

Group A started out with the lower of the two mean levels of suggestibility (13.1 versus 18.0), yet ended up with the higher of the two mean levels of hypnotic induction (29.2 versus 28.1). Our analysis of covariance on this set of data will allow us to answer a what-if question of the type introduced in Part 1: What would have happened if the two groups had started out on an equal footing with respect to primary suggestibility?

---

So this, in brief, is why you would want to bother with the procedures of ANCOVA in a situation of this sort:

• first, to remove from Y the extraneous variability that derives from pre-existing individual differences, insofar as those differences are reflected in the covariate X;_|
  
• and second, to adjust the means of the Y measures to compensate for the fact the groups of subjects started out with different mean levels of the covariate X._|
  

The calculations required to achieve these ends are given in Part 2, along with a few more observations on the Big Picture.