©Richard Lowry, 1999-
All rights reserved.
Subchapter 14a.
The Kruskal-Wallis Test
for 3 or More Independent Samples
- that the scale on which the dependent variable is measured has the properties of an equal interval scale;T
- that the k samples are independently and randomly drawn from the source population(s);T
- that the source population(s) can be reasonably supposed to have a normal distribution; andT
- that the k samples have approximately equal variances.
I will illustrate the Kruskal-Wallis test with an example based on rating-scale data, since this is by far the most common situation in which unequal sample sizes would call for the use of a non-parametric alternative. In this particular case the number of groups
To assess the effects of expectation on the perception of aesthetic quality, an investigator randomly sorts 24 amateur wine aficionados into three groups, A, B, and C, of 8 subjects each. Each subject is scheduled for an individual interview. Unfortunately, one of the subjects of group B and two of group C fail to show up for their interviews, so the investigator must make do with samples of unequal size:
Group|
| A | B | C |
|
6.4 | 6.8 7.2 8.3 8.4 9.1 9.4 9.7
2.5 | 3.7 4.9 5.4 5.9 8.1 8.2
1.3 | 4.1 4.9 5.2 5.5 8.2 mean | 8.2 | 5.5 | 4.9 | | |||
¶Mechanics
The preliminaries of the Kruskal-Wallis test are much the same as those of the Mann-Whitney test described in Subchapter 11a. We begin by assembling the measures from all k samples into a single set of size N. These assembled measures are rank-ordered from lowest (rank#1) to highest (rank#N), with tied ranks included where appropriate; and the resulting ranks are then returned to the sample, A, B, or C, to which they belong and substituted for the raw measures that gave rise to them. Thus, the raw measures that appear in the following table on the left are replaced by their respective ranks, as shown in the table on the right.
| Raw Measures | Ranked Measures|
| A | B | C | A | B | C |
|
6.4 | 6.8 7.2 8.3 8.4 9.1 9.4 9.7
2.5 | 3.7 4.9 5.4 5.9 8.1 8.2
1.3 | 4.1 4.9 5.2 5.5 8.2
11 | 12 13 17 18 19 20 21
2 | 3 5.5 8 10 14 15.5
1 | 4 5.5 7 9 15.5 A, B, C | Combined
| sum of ranks | 131 | 58 | 42 | 231 | average of ranks | 16.4 | 8.3 | 7.0 | 11 | | ||||||||||||
With the Kruskal-Wallis test, however, we take account not only of the sums of the ranks within each group, but also of the averages. Thus the following items of symbolic notation:
| TA = | the sum of the na ranks in group A|
| MA = | the mean of the na ranks in group A |
| TB = | the sum of the nb ranks in group B |
| MB = | the mean of the nb ranks in group B |
| TC = | the sum of the nc ranks in group C |
| MC = | the mean of the nc ranks in group C |
| Tall = | the sum of the N ranks in all groups combined |
| Mall = | the mean of the N ranks in all groups combined | | |||||||||||||
¶Logic and Procedure
·The Measure of Aggregate Group Differences
You will sometimes find the Kruskal-Wallis test described as an "analysis of variance by ranks." Although it is not really an analysis of variance at all, it does bear a certain resemblance to ANOVA up to a point. In both procedures, the first part of the task is to find a measure of the aggregate degree to which the group means differ. With ANOVA that measure is found in the quantity known as SSbg, which is the between-groups sum of squared deviates. The same is true with the Kruskal-Wallis test, except that here the group means are based on ranks rather than on the raw measures. As a reminder that we are now dealing with ranks, we will symbolize this new version of the between-groups sum of squared deviates as SSbg(R). The following table summarizes the mean ranks for the present example. Also included are the sums and the counts (na, nb, nc, and N) on which these means are based.
| A | B | C | All| counts | 8 | 7 | 6 | 21 | sums | 131 | 58 | 42 | 231 | means | 16.4 | 8.3 | 7.0 | 11.0 | |
In Chapters 13 and 14 you saw that the squared deviate for any particular group mean is equal to the squared difference between that group mean and the mean of the overall array of data, multiplied by the number of observations on which the group mean is based. Thus, for each of our current three groups
| A: | 8(16.4—11.0)2 = 233.3 | |||||||
| B: | 7(8.3—11.0)2 = 051.0
|
| C:
| 6(7.0—11.0)2 = 096.0
|
|
| SSbg(R) = 380.3 |
On analogy with the formulaic structures for SSbg developed in Chapters 13 and 14, we can write the conceptual formula for SSbg(R) as
| SSbg(R) =( | Here as well, the subscript "g" means "any particular group." |
and the computational formula as
| SSbg(R) | = | (Tg)2 ng | — | (Tall)2 Na |
With k=3 samples, this latter structure would be equivalent to
| SSbg(R) | = | (TA)2 na | + | (TB)2 nb | + | (TC)2 nc | — | (Tall)2 Na |
For k=4 it would be
| SSbg(R) | = | (TA)2 na | + | (TB)2 nb | + | (TC)2 nc | + | (TD)2 nd | — | (Tall)2 Na |
And so forth for other values of k.
Here, in any event, is how it would work out for the present example. The discrepancy between what we get now and what we got a moment ago (380.3) is due to rounding error in the earlier calculation. As usual, it is the computational formula that is the less susceptible to rounding error, hence the more reliable.
| SSbg(R) | = | (131)2 8 | + | (58)2 7 | + | (42)2 6 | — | (231)2 21
|
| = 378.7 | |||
·The Null-Hypothesis Value of SSbg(R)
The null hypothesis in this or any comparable situation involving several independent samples of ranked data is that the mean ranks of the k groups will not substantially differ. On this account, you might suppose that the null-hypothesis value of SSbg(R), the aggregate measure of group differences, would be simply zero. A moment's reflection, however, will show why this cannot be so.
| A | B | C | x | x x | x x | x |
| N! na! nb! nc! | = | 6! 2! 2! 2! | = 90|
| |
And the values of SSbg(R) produced by these 90 combinations would constitute the sampling distribution of SSbg(R) for this particular case. Of these 90 possible combinations, a few (6) would yield values of SSbg(R) equal to exactly zero. All the rest would produce values greater than zero. (It is mathematically impossible to have a sum of squared deviates less than zero.) Accordingly, the mean of this sampling distribution—the value that observed instances of SSbg(R) will tend to approximate if the null hypothesis is true—is not zero, but something greater than zero.
In any particular case of this sort, the mean of the sampling distribution of SSbg(R) is given by the formula
| (k—1) x | N(N+1) 12
| |
which for the simple case just examined works out as
| (3—1) x | 6(6+1) 12 | = 7.0|
| |
For our main example, we therefore know that the observed value of
| (3—1) x | 21(21+1) 12 | = 77.0|
| |
All that now remains is to figure out how to turn this fact into a rigorous assessment of probability.
·The Kruskal-Wallis Statistic: H
In case you have been girding yourself for some heavy slogging of the sort encountered with the Mann-Whitney test, you can now relax, for the rest of the journey is quite an easy one. The Kruskal-Wallis procedure concludes by defining a ratio symbolized by the letter H, whose numerator is the observed value of SSbg(R) and whose denominator includes a portion of the above formula for the mean of the sampling distribution of SSbg(R). Note that most textbooks give a very different-looking formula for the calculation of H—a rather impenetrable structure to which we will return in a moment. This first version affords a much clearer sense of the underlying concepts.
| H | = | SSbg(R) N(N+1)/12
| |
And now for the denouement. When each of the k samples includes at least 5 observations (that is, when na, nb, nc, etc., are all equal to or greater than 5), the sampling distribution of H is a very close approximation of the chi-square distribution for
For our present example, we can therefore calculate the value of H as
| H | = | SSbg(R) N(N+1)/12 | = | 378.7 21(21+1)/12 | = 9.84|
| |
And then, treating this result as though it were a value of chi-square, we can refer it to the sampling distribution of chi-square with
Theoretical Sampling Distribution of Chi-Square for df=2
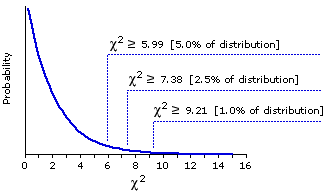
|
·An Alternative Formula for the Calculation of H
I noted a moment ago that textbook accounts of the Kruskal-Wallis test usually give a different version of the formula for H. If you are a beginning student calculating H by hand, I would recommend using the version given above, as it gives you a clearer idea of just what H is measuring. Once you get the hang of things, however, you might find this alternative computational formula a bit more convenient.
| H | = | 12 N(N+1) | ( | (Tg)2 ng | ) | — | 3(N+1)|
| |
In any event, as you can see below, this version yields exactly the same result as the other.
| H | = | 12 21(21+1) | ( | (131)2 8 | + | (58)2 7 | + | (42)2 6 | ) | — | 3(21+1)|
|
|
| = | 9.84 | |
The VassarStats web site has a page that will perform all steps of the Kruskal-Wallis test, including the rank-ordering of the raw measures.
Return to Top of Subchapter 14a
Go to Chapter 15 [One-Way Analysis of Variance for Correlated Samples]
| Home | Click this link only if the present page does not appear in a frameset headed by the logo Concepts and Applications of Inferential Statistics |