©Richard Lowry, 1999-
All rights reserved.
Chapter 3. Introduction to Linear Correlation and Regression
Part 2
[Traducción en español]
The calculations we have just worked through in Part 1 of this chapter were performed on some very small and simple sets of data. Larger, more complex data sets will of course require something more laborious—but the general principles and specific computational procedures are precisely the same, either way. Consider, for example, the data set we referred to at the beginning of the chapter, pertaining to the correlation between the percentage of high school seniors taking the SAT versus average state score on the SAT.
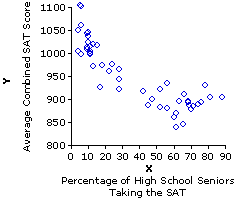
Table 3.2 shows the details of calculation for this data set. As you will see, it requires quite a large number of separate operations, many of which result in multi-digit numerical values. There was a time in the not too distant past when students of statistics had to perform calculations of this sort armed with nothing but paper, pencil, and patience, and it was a very laborious enterprise indeed. But that was then, and this is now. With a fairly inexpensive pocket calculator and a little practice in using it to its full advantage, you can perform complex calculations of this sort with a speed that would have made an earlier generation of statistics students weep with envy. With a computer spreadsheet, and again a little practice, you can do it even faster. With pre-packaged computer software, such as the linear correlation page on the VassarStats website, you can do it with as little time and effort as it takes you to enter the paired values of Xi and Yi.
At any rate, once you perform the operations required to arrive at the following sums (from Table 3.2), all the rest is simple and straightforward:
Given these results from the preliminary number-crunching, you could then (as shown in Table 3.2) easily calculate
SSX = 36,764.88
SSY = 231,478.42
SCXY = —79,672.64
r = —0.86
r2 = 0.74
The Interpretation of Correlation
The interpretation of an observed instance of correlation can take place at two quite distinct levels. The first of these involves a fairly conservative approach that emphasizes the observed fact of covariation and does not go very far beyond this fact. The second level of interpretation builds on the first, but then goes beyond it to consider whether the relationship between the two correlated variables is one of cause and effect. The latter is a potentially more fruitful approach to interpretation, but also a potentially more problematical one.
¶Correlation as Covariation
When you find two variables to be correlated, the fundamental meaning of that fact is that the particular paired instances of Xi and Yi that you have observed tend to co-vary. The positive or negative sign of r, the coefficient of correlation, indicates the direction of covariation, and the magnitude of r2, the coefficient of determination, provides an equal interval and ratio measure of the degree of covariation. Thus, when we find a correlation coefficient ofr=—0.86 for our 1993 SAT data, the fundamental meaning of this numerical fact is that the particular paired instances of Xi and Yi listed in Table 3.2 show some degree of covariation, and that the direction of that covariation is negative, or inverse. When we square r to get the coefficient of determination, r2=0.74, the fundamental meaning of this numerical fact is that the degree of covariation is 74%. That is, 74% of the variance of the Y variable is coupled with variability in the X variable; similarly, 74% of the variance of the X variable is associated with variability in the Y variable. Conversely, you could say that 26% of the variance of the Y variable is not coupled with variability in the X variable, and similarly that 26% of the variance of the X variable is not associated with variability in the Y variable.
The basic concepts involved in this bare-bones covariation interpretation are illustrated in the following diagram. Each of the full circles represents 100% of the variance of either X or Y. In the case of zero correlation there is no tendency for X and Y to co-vary; and thus, as illustrated by the two separated circles at the top, there is zero overlap between the variability of X and the variability of Y. Any non-zero correlation (positive or negative) will reflect the fact that X and Y do tend to co-vary; and the greater the degree of covariation, as measured by r2, the greater the overlap.
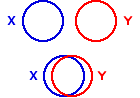
The bottom two circles illustrate the overlap for our observed SAT correlation ofr=—0.86, and more generally for any instance of correlation where r is either —0.86 or +0.86. The area of overlap represents the fact that 74% of the variance of Y is coupled with variability in X, and vice versa; and the areas of non-overlap represent the fact that 26% of the variance of Y is unrelated to variability in X, just as 26% of the variance of X is unrelated to variability in Y. This non-overlapping portion of the variance of either X or Y is spoken of as the residual variance. In general, the proportion of the variance of either variable that is coupled with variability in the other is given by r2, and the proportion of residual variance for either variable is given by 1—r2.
If we were examining correlation simply as a mathematical abstraction, this interpretation is all we would really need. Correlation is covariation, covariation is correlation, and all the rest is just a matter of filling in the details. The next level of interpretation ventures beyond the safe and tidy realm of mathematical abstraction and asks the question: What (if anything) does an observed correlation between two variables have to do with empirical reality? Ex nihilo nihil fit. Freely translated, it means that nothing comes from nowhere, so everything must come from somewhere. Granted that correlation is covariation. The question is, where does the covariation come from?
¶The Question of Cause and Effect
Correlation is a tool, and any tool, if misused, is capable of doing harm. Use a hammer the wrong way, and you will smash your thumb. Use correlation the wrong way, by jumping too quickly, glibly, and simple-mindedly to inferences about cause and effect, and you will arrive at conclusions that are false and misleading. The risk is so great that many statistics instructors and textbooks actively discourage students from even thinking about causal relationships in connection with correlation. Usually it takes the form of a caution: "You cannot infer a causal relationship solely on the basis of an observed correlation." Occasionally, it almost sounds like an eleventh commandment: "Thou shalt not infer causation on the basis of correlation!" The caution is correct. The commandment is much overstated.
If two variables are systematically related to each other as cause and effect, then variation in the cause will produce corresponding variation in the effect, and the two will accordingly show some degree of correlation. There is, for example, a fairly high positive correlation between human height and weight, and for obvious reasons. The taller a person is, the greater the basic mass of the body; and for those inclined to corpulence, the more room there is on the frame of a taller body for adding additional mass. In brief, height and weight are related to each other as cause and effect, and the correlation between the two variables reflects this causal relationship. Alternatively, you could say that the causal relationship between height and weight produces the observed correlation.
But the fact that causal relationships between variables can produce correlations does not entail that a causal relationship lies behind each and every instance of correlation. An observed correlation tells you nothing more than that the two variables co-vary. In some cases the covariation does reflect a causal relationship between the variables, and in other cases it does not. The trick is in determining which is which. An observed correlation between two variables does give you grounds for considering the possibility of a causal relationship—but that possibility must then be carefully and cautiously weighed in the balance of whatever other information you might have about the nature of the two variables.
Whenever you find two variables, X and Y, to be correlated, the basic possibilities concerning the question of cause and effect are the following:
Possibility 1. By the time you complete the chapters of this webtext, you will have raised the general question of Possibility 1 so often that it will seem as though you were born with it. When you sample the events of nature and observe a pattern, it may be that the pattern of the sample reflects a corresponding pattern in the entire population from which the sample is drawn. But then again, it may be that the pattern observed in the sample is only a fluke, the result of nothing more than mere chance coincidence. This, of course, is the general question of statistical significance, and once you get past the current chapter, there will be scarcely a page in this text that does not refer to it in one way or another. We will broach the question in somewhat greater detail toward the end of this chapter. Meanwhile, suffice it to say that before you even begin thinking about the issue of cause and effect, you first need to determine whether it is reasonable to assume that the observed correlation comes from anything other than mere chance coincidence. The remaining possibilities presuppose that this determination has been validly made in the affirmative.
Possibility 2. First, of course, is the possibility that there is a causal relationship between X and Y, either direct or indirect, such that variation in X produces variation in Y
or alternatively, such that variation in Y produces variation in X
In the latter case, you would do well to switch the X and Y labels of your variables; for as we noted earlier, the convention is to reserve "Y" for the dependent variable (the effect) and "X" for the independent variable (the cause).
At any rate, in seeking to determine whether an observed XY correlation betokens the existence of a causal relationship, the logical first step would be to rule out the possibility that it reflects something other than a causal relationship between X and Y. Remember, we are assuming here that the question of statistical significance has already been answered in the affirmative. The observed correlation is assumed to come from something more than mere chance coincidence; and if that something is not a causal relationship between X and Y, then what else could it possibly be?
Possibility 3. If you examine the records of the city of Copenhagen for the ten or twelve years following World War II, you will find a strong positive correlation between (i) the annual number of storks nesting in the city, and (ii) the annual number of human babies born in the city. Jump too quickly to the assumption of a causal relationship, and you will find yourself saddled with the conclusion either that storks bring babies or that babies bring storks. Or consider this one. If you examine the vital statistics of any country over a period of years, you will find a virtually perfect positive correlation between (i) the annual number of live male births, and (ii) the annual number of live female births. Do baby boys bring baby girls, or is it the other way around?
In both of these examples what you have is a situation where two variables end up as correlated, not because one is influencing the other, but rather because both are influenced by a third variable, Z, that is not being taken into account. That is, the causal relationship here is notX·····>Y or X<·····Y, but rather
For the male-female births example, the third variable is quite simply the overall annual birth rate. More babies are born in some years than in others. But no matter what the birth rate in any given year, the proportions of male and female births tend to remain fairly constant, with male births slightly outnumbering female births. (In the United States for recent decades it has been in the vicinity of 51.25% males and 48.75% females.) Thus, a relatively high birth rate will bring with it relatively high numbers of both male and female births, and a relatively low birth rate will bring relatively low numbers of both male and female births.
In short, the annual numbers of male and female births are correlated with each other only because they are both correlated with fluctuations in the annual birth rate.
The third variable for the correlation between storks and babies does not leap off the page quite so conspicuously, but it is there all the same. During the ten or twelve years following World War II, the populations of most western European cities steadily grew as a result of migrations from surrounding rural areas. There was also that spurt of fecundity known as the post-war baby boom. Here is how it worked out for the city of Copenhagen, which is also home to annually fluctuating numbers of storks. As population increased, there were more people to have babies, and therefore more babies were born. Also as population increased, there was more building construction to accommodate it, which in turn provided more nesting places for storks; hence increasing numbers of storks.
Notice in this kind of situation that it makes no sense to speak of X as the independent variable and Y as the dependent variable. For in fact, X and Y are both independent of each other and dependent on variable Z.
¶Interpreting the SAT Correlation
So what shall we make, in this context, of our observed correlation between
which you will recall was measured as r=—0.86 and r2=0.74? Question one: Is the observed correlation statistically significant—i.e., is it unlikely to have occurred by mere chance coincidence? For the moment I will have to ask you to take my word that it is. Through procedures that we will examine later, you will see that the mere-chance likelihood of finding a correlation this strong for a bivariate sample of size N=50 is very tiny indeed. Question two: Is there anything other than a straightforward X·····>Y causal relationship that could plausibly account for the observed correlation? Is it possible, for example, that X and Y are correlated with each other only because they are both being influenced by some third variable, Z? Alternatively, is it possible that X and Y are influencing each other reciprocally? I think you will agree that the possibility of reciprocal influence is unlikely, as it is difficult to imagine how a state's average score on the SAT in a given year could retroactively influence the percentage of high school seniors in the state who took the test. The possibility of a third variable, Z, cannot be quite so quickly ruled out, though it is not immediately obvious just what Z might be. Certainly there are other variables that play a role in the situation, but that does not necessarily mean that they are influencing X and Y separately, according to the paradigm
For all of the possible candidates for Z that I can think of (economic factors, demographic factors, geographic factors, etc.), the scenario is one in which Z would influence first X, and then Y through the mediation of X, according to the paradigm
Here is one fairly obvious example. Few if any high school seniors take the SAT for the sheer fun of it. Those who take it do so because they are applying to colleges that require the SAT. In some states it is a smaller percentage who apply to such colleges, hence a smaller percentage who take the SAT; and in other states it is a larger percentage who apply to such colleges, hence a larger percentage who take the SAT. Z is the state percentage of seniors applying to colleges that require the SAT; X is the state percentage of seniors who take the SAT; and the positive correlation that we would surely find between these two variables, if we were to measure it, would clearly betoken a relationship of cause and effect(Z····>X).
In any event, from everything we know about the two primary variables, X and Y, in this situation, the possibility of a straightforwardX····>Y causal relationship is an entirely plausible one. Imagine two states, A and B, whose respective percentages of high school seniors taking the SAT are A=5% and B=65%. Now the 5% of seniors in state A that happen to take the SAT may not represent precisely the top 5% in that state, but surely they are more likely to represent the top 10 or 15% than the top 60 or 70%. On the other hand, there is no way at all that the 65% who take the test in state B could come mostly from the top 10 or 15% of the high school seniors in that state, nor even from the top 25%. In fact, nearly a quarter of them could not possibly come even from the top 50%. So here is our presumed causal connection in a nutshell: A smaller percentage of students taking the SAT will tend to represent the upper portion of the scale of academic prowess, and will thus tend to produce a higher state average SAT score; whereas a larger percentage of students taking the test will tend to include not only students near the top of the scale, but also others not so near the top, and will thus tend to produce a lower state average SAT score.
Assuming that theX····>Y causal relationship is as I have described it, we could then link up again with the covariation interpretation of correlation and observe the following (recall that r=—0.86 and r2=0.74). Of the total variability that exists among the 50 states with respect to average SAT scores, 74% is associated with variability in the percentages of high school seniors taking the SAT. In effect, 74% of the state-by-state differences in average SAT scores are explained by the fact that different states have different percentages of high school seniors taking the test. And that is 74% that does not need to be explained by presumed quality differences among state educational systems—unless you fancy the rather far-fetched notion that the most effective educational systems are those that produce the smallest percentages of students applying to colleges that require the SAT. Assuming that this latter notion is as preposterous as it seems, the maximum proportion of state-by-state variability in average SAT scores that could conceivably be due to differences among state educational systems is the 26% that is not explained by state-by-state differences in the percentage of seniors taking the SAT. And please note that this is only the maximum possible proportion. It could well turn out that measurable differences among state educational systems account for only a fraction of the 26% residual variance of Y, if indeed they account for any part of it at all.

Table 3.2 shows the details of calculation for this data set. As you will see, it requires quite a large number of separate operations, many of which result in multi-digit numerical values. There was a time in the not too distant past when students of statistics had to perform calculations of this sort armed with nothing but paper, pencil, and patience, and it was a very laborious enterprise indeed. But that was then, and this is now. With a fairly inexpensive pocket calculator and a little practice in using it to its full advantage, you can perform complex calculations of this sort with a speed that would have made an earlier generation of statistics students weep with envy. With a computer spreadsheet, and again a little practice, you can do it even faster. With pre-packaged computer software, such as the linear correlation page on the VassarStats website, you can do it with as little time and effort as it takes you to enter the paired values of Xi and Yi.
At any rate, once you perform the operations required to arrive at the following sums (from Table 3.2), all the rest is simple and straightforward:
Sums of| Xi | Yi |
| Xi2 | Yi2 |
| XiYi | 1,816 | 47,627 | 102,722 | 45,598,101 | 1,650,185 | | ||||||
Given these results from the preliminary number-crunching, you could then (as shown in Table 3.2) easily calculate
SSY = 231,478.42
SCXY = —79,672.64
r = —0.86
r2 = 0.74
The Interpretation of Correlation
The interpretation of an observed instance of correlation can take place at two quite distinct levels. The first of these involves a fairly conservative approach that emphasizes the observed fact of covariation and does not go very far beyond this fact. The second level of interpretation builds on the first, but then goes beyond it to consider whether the relationship between the two correlated variables is one of cause and effect. The latter is a potentially more fruitful approach to interpretation, but also a potentially more problematical one.
¶Correlation as Covariation
When you find two variables to be correlated, the fundamental meaning of that fact is that the particular paired instances of Xi and Yi that you have observed tend to co-vary. The positive or negative sign of r, the coefficient of correlation, indicates the direction of covariation, and the magnitude of r2, the coefficient of determination, provides an equal interval and ratio measure of the degree of covariation. Thus, when we find a correlation coefficient of
The basic concepts involved in this bare-bones covariation interpretation are illustrated in the following diagram. Each of the full circles represents 100% of the variance of either X or Y. In the case of zero correlation there is no tendency for X and Y to co-vary; and thus, as illustrated by the two separated circles at the top, there is zero overlap between the variability of X and the variability of Y. Any non-zero correlation (positive or negative) will reflect the fact that X and Y do tend to co-vary; and the greater the degree of covariation, as measured by r2, the greater the overlap.
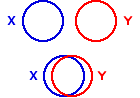
The bottom two circles illustrate the overlap for our observed SAT correlation of
If we were examining correlation simply as a mathematical abstraction, this interpretation is all we would really need. Correlation is covariation, covariation is correlation, and all the rest is just a matter of filling in the details. The next level of interpretation ventures beyond the safe and tidy realm of mathematical abstraction and asks the question: What (if anything) does an observed correlation between two variables have to do with empirical reality? Ex nihilo nihil fit. Freely translated, it means that nothing comes from nowhere, so everything must come from somewhere. Granted that correlation is covariation. The question is, where does the covariation come from?
¶The Question of Cause and Effect
Correlation is a tool, and any tool, if misused, is capable of doing harm. Use a hammer the wrong way, and you will smash your thumb. Use correlation the wrong way, by jumping too quickly, glibly, and simple-mindedly to inferences about cause and effect, and you will arrive at conclusions that are false and misleading. The risk is so great that many statistics instructors and textbooks actively discourage students from even thinking about causal relationships in connection with correlation. Usually it takes the form of a caution: "You cannot infer a causal relationship solely on the basis of an observed correlation." Occasionally, it almost sounds like an eleventh commandment: "Thou shalt not infer causation on the basis of correlation!" The caution is correct. The commandment is much overstated.
If two variables are systematically related to each other as cause and effect, then variation in the cause will produce corresponding variation in the effect, and the two will accordingly show some degree of correlation. There is, for example, a fairly high positive correlation between human height and weight, and for obvious reasons. The taller a person is, the greater the basic mass of the body; and for those inclined to corpulence, the more room there is on the frame of a taller body for adding additional mass. In brief, height and weight are related to each other as cause and effect, and the correlation between the two variables reflects this causal relationship. Alternatively, you could say that the causal relationship between height and weight produces the observed correlation.
But the fact that causal relationships between variables can produce correlations does not entail that a causal relationship lies behind each and every instance of correlation. An observed correlation tells you nothing more than that the two variables co-vary. In some cases the covariation does reflect a causal relationship between the variables, and in other cases it does not. The trick is in determining which is which. An observed correlation between two variables does give you grounds for considering the possibility of a causal relationship—but that possibility must then be carefully and cautiously weighed in the balance of whatever other information you might have about the nature of the two variables.
Whenever you find two variables, X and Y, to be correlated, the basic possibilities concerning the question of cause and effect are the following:
Possibility 1. By the time you complete the chapters of this webtext, you will have raised the general question of Possibility 1 so often that it will seem as though you were born with it. When you sample the events of nature and observe a pattern, it may be that the pattern of the sample reflects a corresponding pattern in the entire population from which the sample is drawn. But then again, it may be that the pattern observed in the sample is only a fluke, the result of nothing more than mere chance coincidence. This, of course, is the general question of statistical significance, and once you get past the current chapter, there will be scarcely a page in this text that does not refer to it in one way or another. We will broach the question in somewhat greater detail toward the end of this chapter. Meanwhile, suffice it to say that before you even begin thinking about the issue of cause and effect, you first need to determine whether it is reasonable to assume that the observed correlation comes from anything other than mere chance coincidence. The remaining possibilities presuppose that this determination has been validly made in the affirmative.
Possibility 2. First, of course, is the possibility that there is a causal relationship between X and Y, either direct or indirect, such that variation in X produces variation in Y
| X | ·····> | Y |
| X | <····· | Y |
At any rate, in seeking to determine whether an observed XY correlation betokens the existence of a causal relationship, the logical first step would be to rule out the possibility that it reflects something other than a causal relationship between X and Y. Remember, we are assuming here that the question of statistical significance has already been answered in the affirmative. The observed correlation is assumed to come from something more than mere chance coincidence; and if that something is not a causal relationship between X and Y, then what else could it possibly be?
Possibility 3. If you examine the records of the city of Copenhagen for the ten or twelve years following World War II, you will find a strong positive correlation between (i) the annual number of storks nesting in the city, and (ii) the annual number of human babies born in the city. Jump too quickly to the assumption of a causal relationship, and you will find yourself saddled with the conclusion either that storks bring babies or that babies bring storks. Or consider this one. If you examine the vital statistics of any country over a period of years, you will find a virtually perfect positive correlation between (i) the annual number of live male births, and (ii) the annual number of live female births. Do baby boys bring baby girls, or is it the other way around?
In both of these examples what you have is a situation where two variables end up as correlated, not because one is influencing the other, but rather because both are influenced by a third variable, Z, that is not being taken into account. That is, the causal relationship here is not
| Z ··· | ····>X ····>Y |
| total number of births ··· | ····>number of male births ····>number of female births |
The third variable for the correlation between storks and babies does not leap off the page quite so conspicuously, but it is there all the same. During the ten or twelve years following World War II, the populations of most western European cities steadily grew as a result of migrations from surrounding rural areas. There was also that spurt of fecundity known as the post-war baby boom. Here is how it worked out for the city of Copenhagen, which is also home to annually fluctuating numbers of storks. As population increased, there were more people to have babies, and therefore more babies were born. Also as population increased, there was more building construction to accommodate it, which in turn provided more nesting places for storks; hence increasing numbers of storks.
| increasing population ··· | ····>more buildings ····> ····>increasing numbers of storks ····>more baby makers ····>····>increasing numbers of babies |
¶Interpreting the SAT Correlation
So what shall we make, in this context, of our observed correlation between
| X = | percentage of high school seniors within a state taking the SAT, and| Y = | the state's average combined score on the SAT | |
| Z ··· | ····>X ····>Y | [I.e., Z····>X and Z····>Y but not X····>Y or Y····>X] |
| Z····>X····>Y |
[I.e., Z····>X and X····>Y] |
Here is one fairly obvious example. Few if any high school seniors take the SAT for the sheer fun of it. Those who take it do so because they are applying to colleges that require the SAT. In some states it is a smaller percentage who apply to such colleges, hence a smaller percentage who take the SAT; and in other states it is a larger percentage who apply to such colleges, hence a larger percentage who take the SAT. Z is the state percentage of seniors applying to colleges that require the SAT; X is the state percentage of seniors who take the SAT; and the positive correlation that we would surely find between these two variables, if we were to measure it, would clearly betoken a relationship of cause and effect
In any event, from everything we know about the two primary variables, X and Y, in this situation, the possibility of a straightforward
Assuming that the
Return to Top of Part 2
Go to Chapter 3, Part 3
| Home | Click this link only if the present page does not appear in a frameset headed by the logo Concepts and Applications of Inferential Statistics |