2x2 Contingency Table

For a 2x2 Contingency Table:

·Phi Coefficient of Association
·Chi-Square Test of Association
·Fisher Exact Probability Test

For a table of frequency data cross-classified according to two categorical variables, X and Y, each of which has two levels or subcategories, this page will

calculate the Phi coefficient of association;_T
perform a chi-square test of association, if the sample size is not too small; and_T
perform the Fisher exact probability test, if the sample size is not too large. [Although the Fisher test is traditionally used with relatively small samples, the programming for this page will handle fairly large samples, up to about n=1000, depending on how the frequencies are arrayed within the four cells.]_T
For intermediate values of n, the chi-square and Fisher tests will both be performed.

To proceed, enter the values of X₀Y₁, X₁Y₁, etc., into the designated cells. When all four cell values have been entered, click the «Calculate» button. To perform a new analysis with a new set of data, click the «Reset» button.

The logic and computational details of the Chi-Square and Fisher tests are described in Chapter 8 and Subchapter 8a, respectively, of Concepts and Applications. A briefer account of the Fisher test will be found toward the bottom of this page.

Data Entry_T

		X			Expected Cell Frequencies per Null Hypothesis
		0	1	Totals
Y	1
	0
Totals

Calculate Reset

	Chi-Square		Chi-square is calculated only if all expected cell frequencies are equal to or greater than 5. The Yates value is corrected for continuity; the Pearson value is not. Both probability estimates are non-directional.
Phi	Yates	Pearson

P

Fisher Exact Probability Test:_T

P	one-tailed
P	two-tailed

Home

Click this link only if you did not arrive here via the VassarStats main page.

Fisher Exact Probability Test: Logic and Procedure
Consider a 2x2 contingency table of the sort described above, with the cell frequencies represented by a, b, c, d, and the marginal totals represented by a+b, c+d, a+c, b+d, and n.

	0	1	Totals
1	a	b	a+b
0	c	d	c+d
Totals	a+c	b+d	n

If there were no systematic association between the variables A and B within the population from which the cell frequencies are randomly drawn, the probability of any particular possible array of cell frequencies, a, b, c, d, given fixed values for the marginal totals a+b, c+d, etc., would be given by the hypergeometric rule

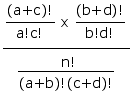
which for computational purposes reduces to

Also, the degree of disproportion within any array of cell frequencies—in effect, the degree of ostensible association between variables A and B within the sample—can be measured by the absolute difference

For any particular observed array of cell frequencies, the programming embedded in this page calculates the probability of that particular array plus the probabilities of all other possible arrays whose degree of disproportion is equal to or greater than that of the observed array. Thus, for the observed array

2	7	9
8	2	10
10	9	19

the one-tailed probability would be the sum of the separate probabilities for the arrays

		probability
2	7
8	2	0.01754
1	8
9	1	0.00097
0	9
10	0	0.00001

sum = 0.01852			(one-tailed probability)

And the two-tailed probability would be that sum plus the sum of the separate probabilities for the arrays of equal or greater disproportion at the other extreme:

		probability
8	1
2	8	0.00438
9	0
1	9	0.00011

sum = 0.00449

two-tailed probability = 0.01852 + 0.00449 = 0.02301

Return to Top