Fit to Poisson

Fitting to a Poisson Distribution

If you have visited this page before and wish to skip the preamble, click here to go directly to the calculator.

The frequency distributions of relatively rare or improbable events tend to approximate the form of a Poisson distribution, the defining characteristic of which is that its mean and variance are identical.

k	Observed Frequency
0 1 2 3 4	28 20 8 3 1

Consider, for example, the number of micro- organisms of a certain type found within each of N=60 squares of a hemocytometer. The possible outcomes are k=0 in a square, k=1, k=2, and so forth. Suppose there are 28 squares containing none of the organisms, 20 squares containing 1 organism, and so on, as shown in the adjacent table. The mean number of micro- organisms per square in this distribution is .82, with a variance of .92.

As shown in Graph A, below, the fit between the observed distribution and the theoretical Poisson distribution defined by mean=variance=.82 is a fairly close one. However, there are other Poisson distributions for which the fit is even closer. The most closely fitting of all is the one shown in Graph B, defined by mean=variance=.76.

Observed distribution fitted to a theoretical Poisson distribution with

	A. mean=variance=.82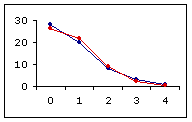	B. mean=variance=.76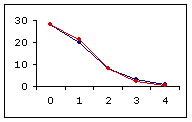
	observed frequency expected frequency

The programming on this page will find the Poisson distribution that most closely fits an observed frequency distribution, as determined by the method of least squares (i.e., the smallest possible sum of squared distances between the observed frequencies and the Poisson expected frequencies). To proceed, enter the observed frequencies for each relevant value of k, then click the 'Calculate' button. A frequency of zero can either be entered as numeral 0 or left blank.

k	Observed		Fitted Poisson
k	Frequency	Proportion	Probability	Expected Frequency

mean of observed sample = ^Tvariance of observed sample =
mean and variance of fitted Poisson distribution =
observed vs expected frequencies proportion of linear covariance: r² =
To see the outlines of the Poisson distribution to which your data have been fitted, click here and enter at the prompt.

Home

Click this link only if you did not arrive here via the VassarStats main page.