For

a situation in which independent binomial events are randomly sampled in sequence, this page will calculate
|
|
|
| (a)
| the probability that you will end up with exactly k instances of the outcome in question, with the final (kth) instance occurring on trial N; and
|
|
|
| (b)
| the probability that you will have to sample at least N events before finding the kth instance of the outcome.
|
| |
For example:
Q
(a)
|
Assuming the probability of a Heads outcome on any particular toss of a coin to be .50: In a series of coin tosses, how likely is it that the 4th instance of a Heads outcome will occur on the 4th toss, the 5th toss, the 6th toss, etc?
k=4; N=4, 5, 6, etc.
|
Assuming the incidence of a certain genetic characteristic within a population to be 8.2% (.082): If a number of randomly selected subjects are tested in sequence, how likely is it that the 3rd instance of the characteristic will be found with the 3rd subject, the 4th, the 5th, etc?
k=3; N=3, 4, 5, etc.
|
(b)
|
If the probability of a Heads outcome on any particular toss of a coin truly is .50: In a series of coin tosses, how likely is it that you would have to toss the coin at least N times (N=4, 5, 6, etc.) before ending up with k=4 heads?
|
If the incidence of the genetic characteristic within the population truly is .082: How likely is it that you would have to sample at least N subjects (N=3, 4, 5, etc.) before finding k=3 subjects that display the characteristic?
|
The probabilities for (a) are calculated for N=k through N=k+25, according to the Pascal rule, also known as the negative binomial:
|
|
|
|
P(a) =
|
(N-1)!
(k-1)! (N-k)!
|
pk (1-p)N-kk
|
| |
where p is the known or hypothetical probability that the outcome in question will occur on any particular trial. The probabilities for (b) are then constructed as
|
|
|
|
P(b) = 1-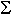 P(a)* P(a)*
|
| |
with
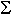
P
(a)* equal to the sum of all values of P
(a) for N=k through N-1.
Note that with k=1, P(a) and P(b) are equivalent to the probabilities of the geometric distribution defined by pk (1-p)N-k. In this case, P(a) is the probability that the first instance of the outcome will occur on the Nth trial and P(b) is the probability that you will have to sample at least N events before finding the first instance of the outcome.
|
To proceed, enter the values of k and p into the designated cells, then click the «Calculate» button. k must be an integer between 1 and 150, inclusive. The value entered for p can be either a decimal fraction such as .25 or a common fraction such as 1/4.
| Home
| Click this link only if you did not arrive here via the VassarStats main page.
|
©Richard Lowry 2001-
All rights reserved.
 a situation in which independent binomial events are randomly sampled in sequence, this page will calculate
a situation in which independent binomial events are randomly sampled in sequence, this page will calculate
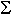 P(a)* equal to the sum of all values of P(a) for N=k through N-1.
P(a)* equal to the sum of all values of P(a) for N=k through N-1.