Analysis of Covariance for 3 Independent Samples
For Importing Data from a Spreadsheet
Importing Data from a Spreadsheet
This page will perform an analysis of covariance for three independent samples, A, B, and C, where
Then return to this page, click the cursor into the data-entry field for Sample A, below, and perform the 'Paste' operation. Do the same for the other two samples in your analysis, then click the 'Calculate' button.
For each sample, make sure that the final entry is not followed by an extra line. (An extra line after the final entry in a sample will be interpreted as an extra data entry whose value is zero.) After all values for a sample have been entered, click the cursor immediately to the right of the final entry in the list, then press the down-arrow key. If an extra line is present, the cursor will move downward. Extra lines can be removed by pressing the down arrow key until the cursor no longer moves, and then pressing the 'Backspace' key (on a Mac platform, 'delete') until the cursor stands immediately to the right of the final entry.
Data Entry:
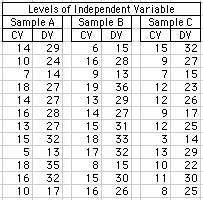
CV = concomitant variable [left column in each sample]
DV = dependent variable [right column in each sample]
ANCOVA Summary
Test for homogeneity of regressions:
©Richard Lowry 2001-
All rights reserved.
|
The logic and computational details of the one-way independent-samples ANCOVA are described in Chapter 17 of Concepts and Applications. |
This page will perform an analysis of covariance for three independent samples, A, B, and C, where
- A, B, and C represent three quantitative or categorical levels of the independent variable;
- DV = the dependent variable of interest; and
- CV = the concomitant variable whose effects one wishes to bring under statistical control.
 |
For each sample, make sure that the final entry is not followed by an extra line. (An extra line after the final entry in a sample will be interpreted as an extra data entry whose value is zero.) After all values for a sample have been entered, click the cursor immediately to the right of the final entry in the list, then press the down-arrow key. If an extra line is present, the cursor will move downward. Extra lines can be removed by pressing the down arrow key until the cursor no longer moves, and then pressing the 'Backspace' key (on a Mac platform, 'delete') until the cursor stands immediately to the right of the final entry.
Data Entry:
CV = concomitant variable [left column in each sample]
DV = dependent variable [right column in each sample]
Levels of Independent Variable
| Sample A
| Sample B
| Sample C
|
|
|
| | |||||
Dependent Variable
| Sample
|
| Total
| A
| B
| C
| n
| | |||||||||||
| Aggregate Correlation within Samples: CV vs DV
| |||
ANCOVA Summary
| Source | SS | df | MS | F | P
| adjusted means
| adjusted error
| adjusted total
| |
Test for homogeneity of regressions:
| Source | SS | df | MS | F | P
| between | regressions remainder
| adjusted error
| |
| Home | Click this link only if you did not arrive here via the VassarStats main page. |
©Richard Lowry 2001-
All rights reserved.